
活动:学生很容易回忆起利用指数函数、对数函数的大小比较,这很好,充分利用学生的知识迁移有利于学生能力的快速提高.本例是余弦,只需将角化为同一个单调区间,然后根据单调性比较大小即可.课堂上仍是让学生自己独立地去操作,教师点拨、纠错,对思考方法不对的学生给予帮助指导.
解:cos(-![]() )=cos
)=cos![]() =cos
=cos![]() ,cos(-
,cos(-![]() )=cos(
)=cos(![]() )=cos
)=cos![]() .因为0<
.因为0<![]() <
<![]() <π,且函数y=cosx,x∈[0,π]是减函数,所以cos
<π,且函数y=cosx,x∈[0,π]是减函数,所以cos![]() >cos
>cos![]() ,即cos(-
,即cos(-![]() )<cos(-
)<cos(-![]() ).
).
点评:推进本例时应提醒学生注意,在今后遇到的三角函数值大小比较时,必须将已知角化为同一个单调区间.其次要注意首先大致的判断一下有没有符号不同的情况,以便快速解题,如本例中,cos![]() >0,cos
>0,cos![]() <0,显然大小立判.
<0,显然大小立判.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源:2014届浙江省高一下学期期中考试数学试卷(解析版) 题型:解答题
已知函数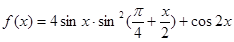 ,
,
(1)设常数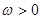 ,若
,若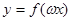 在区间
在区间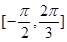 上是增函数,求
上是增函数,求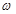 的取值范围;
的取值范围;
(2)设集合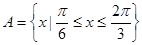 ,
,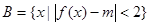 ,若
,若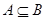 ,求
,求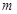 的取值范围.
的取值范围.
【解析】本试题主要考查了三角函数的性质的运用以及集合关系的运用。
第一问中利用
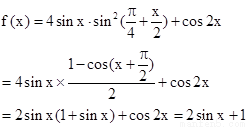
利用函数的单调性得到,参数的取值范围。
第二问中,由于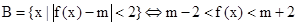 解得参数m的取值范围。
解得参数m的取值范围。
(1)由已知
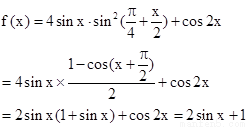
又因为常数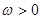 ,若
,若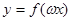 在区间
在区间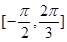 上是增函数故参数
上是增函数故参数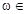

(2)因为集合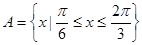 ,
,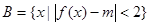 ,若
,若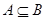
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com