Question

13．已知圆C：x²+y²+2x-4y+3=0．
（1）若不过原点的直线l与圆C相切，且在x轴、y轴上截距相等，求直线l的方程；
（2）从圆C外一点P向圆引一条切线，切点为M，O为坐标原点，且MP=OP，求点P的轨迹方程．

Answer 1

分析 （1）把圆的方程化为标准方程，找出圆心坐标和半径，由直线l不过原点，得到该直线在坐标轴上的截距不为0，设出直线l的截距式方程，利用点到直线的距离公式表示出圆心到直线的距离d，让d等于圆的半径列出关于a的方程，求出方程的解可得到a的值，确定出直线l的方程；
（2）由切线的性质，得到三角形PCM为直角三角形，利用勾股定理得到|PC|²=|PM|²+r²，表示出|PM|²，由|PM|=|PO|，进而得到|PO|²，由设出的P的坐标和原点坐标，利用两点间的距离公式表示出|PO|，可得出|PO|²，两者相等，化简可得点P的轨迹方程．

解答 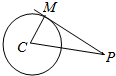解：（1）C：（x+1）²+（y-2）²=2，显然圆心C（-1，2），半径r=$\sqrt{2}$，
∵不过原点的直线l在x轴、y轴上截距相等，
∴不妨设l：$\frac{x}{a}+\frac{y}{a}$=1，即x+y-a=0；
又直线l与圆C相切，∴$\frac{|-1+2-a|}{\sqrt{2}}$=$\sqrt{2}$，
∴a=3或-1，
∴l：x+y-3=0或x+y+1=0；
（2）由题如图，PM与圆C相切于M，∴PM⊥CM，
设P（x，y），由MP=OP得：OP²=MP²=CP²-r²，
∴x²+y²=（x+1）²+（y-2）²-2，
整理得：2x-4y+3=0即为所求．

点评 此题考查了圆的切线方程，以及动点的轨迹方程，涉及的知识有：圆的标准方程，点到直线的距离公式，直线的截距式方程，切线的性质，勾股定理以及两点间的距离公式，当直线与圆相切时，圆心到直线的距离等于圆的半径，常常利用切线长，圆的半径及圆心到圆外点的距离构造直角三角形来解决问题．