Question

如图，点D，E，F分别是四面体S－ABC的棱CA，CB，CS的中点，过点C作一直线分别交AB，DE于点G，H，连接SG，FH．

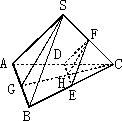
求证：SG∥FH．

Answer 1

答案：
解析：

分析：观察图形，易判定平面FDE∥平面SAB，而SG，FH是第三个平面SGC与上述两个平行平面的交线，于是要证SG∥FH，可利用面面平行的性质定理． 　　证明：由题意知，EF为△SBC的中位线， 　　所以EF∥BS． 　　因为EF平面SAB，SB平面SAB， 　　所以EF∥平面SAB． 　　同理可得DF∥平面SAB． 　　又EF∩DF＝F， 　　所以平面DEF∥平面SAB． 　　又平面SGC∩平面SAB＝SG，平面SGC∩平面DEF＝FH， 　　由平面与平面平行的性质定理，得SG∥FH． 　　点评：应用面面平行的性质定理证明线线平行的关键是：先找到两个平行平面(有时需证明)，再找第三个与它们相交的平面．而第三个平面与两个平行平面的交线就是需要证明的两平行线，于是，由面面平行推知线线平行． 　　解决空间平行问题最根本的是学会转化，此外需要平面几何知识作基础．同学们在学习中要善于思考和总结，这样，才能提高自己的解题能力．