
如图所示,已知△OFQ的面积为S,且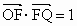 ,若
,若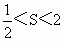 ,求向量
,求向量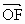 与
与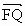 的夹角θ的取值范围.
的夹角θ的取值范围.

科目:高中数学 来源: 题型:
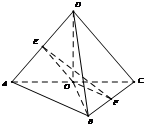 把正方形ABCD沿其对角线AC折成直二面角D-AC-B后,连接BD,得到如图所示的几何体,已知点O、E、F分别为线段AC、AD、BC的中点.
把正方形ABCD沿其对角线AC折成直二面角D-AC-B后,连接BD,得到如图所示的几何体,已知点O、E、F分别为线段AC、AD、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
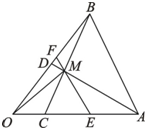 如图所示,在△ABC中,
如图所示,在△ABC中,| OC |
| 1 |
| 4 |
| OA |
| OD |
| 1 |
| 2 |
| OB |
| OA |
| OB |
| OM |
| OE |
| OA |
| OF |
| OB |
| 1 |
| p |
| 3 |
| q |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知点F(1,0),直线l:x=2,设动点P到直线l的距离为d,已知|PF|=
已知点F(1,0),直线l:x=2,设动点P到直线l的距离为d,已知|PF|=
| ||
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| PF |
| OF |
| 1 |
| 3 |
| OP |
| OF |
| GF |
| FC |
| MP |
. |
| PF |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省成都市高三第一次模拟文科数学卷 题型:解答题
把正方形ABCD沿其对角线AC折成二面角DACB后,连结BD,得到如图所示的几何体,已知点O、E、F分别为线段AC、AD、BC的中点。
(I)求证:AB//平面EOF;
(II)求二面角EOFB的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com