(Ⅰ)解:∵数列{an}满足:a
n>0,且对一切n∈N
*,有a
13+a
23+…+a
n3=S
n2,…①
所以a
13+a
23+…+a
n3+a
n+13=S
n+12,…②
①-②得a
n+13=S
n+12-S
n2=a
n+1(S
n+1+S
n),
则a
n+12=S
n+1+S
n=a
n+1+2S
n,
所以a
n+12-a
n+1=2S
n,
又a
n+12-a
n+1=2S
n=2S
n+1-2a
n+1,
所以a
n+12+a
n+1=2S
n+1…③
则a
n2+a
n=2S
n…④
③-④得2a
n+1=(a
n+12-a
n2)+(a
n+1-a
n),
从而a
n+1-a
n=1.
又由已知易得a
1=1,所以数列{a
n}是以首项为a
1=1,公差为1的等差数列
所以a
n=n.
(Ⅱ)证明:∵a
n=n,∴
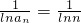
,
令f(x)=lnx-x+1,x>1
∵f'(x)=

-1=

,
∴f(x)单调递减,
那么f(x)<f(1)=0,即lnx<x-1
∴当n≥2,n∈N
*时,0<lnn<n-1,
∴
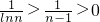
,
∵当n≥2,n∈N时,
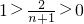
,
∴两式相乘有
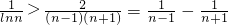
,…(9分)
∴
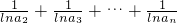
=
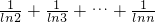
>
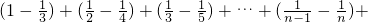
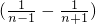
,
=1+

-

=
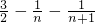
=
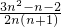
(n≥2,n∈N
*).…(12分)
分析:(Ⅰ)由数列{an}满足:a
n>0,且对一切n∈N
*,有a
13+a
23+…+a
n3=S
n2,知a
13+a
23+…+a
n3+a
n+13=S
n+12,所以a
n+13=S
n+12-S
n2=a
n+1(S
n+1+S
n),a
n+12-a
n+1=2S
n,由a
n+12+a
n+1=2S
n+1,知a
n2+a
n=2S
n.所以2a
n+1=(a
n+12-q
n2)+(a
n+1-a
n),由此能求出a
n=n.
(Ⅱ)由a
n=n,知
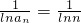
,由当n≥2,n∈N
*时,0<lnn<n-1,知
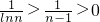
,由当n≥2,n∈N时,
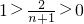
,知
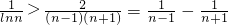
,由上此能够证明
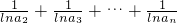
>
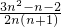
.
点评:本题考查数列与不等式的综合应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.

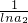 +
+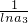 +…
+…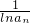 >
>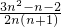 (n≥2,n∈N*).
(n≥2,n∈N*).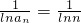 ,
, -1=
-1= ,
,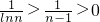 ,
,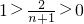 ,
,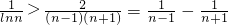 ,…(9分)
,…(9分)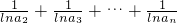
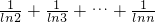
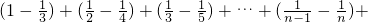
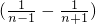 ,
, -
-
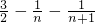
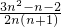 (n≥2,n∈N*).…(12分)
(n≥2,n∈N*).…(12分)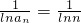 ,由当n≥2,n∈N*时,0<lnn<n-1,知
,由当n≥2,n∈N*时,0<lnn<n-1,知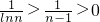 ,由当n≥2,n∈N时,
,由当n≥2,n∈N时,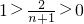 ,知
,知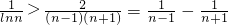 ,由上此能够证明
,由上此能够证明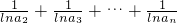 >
>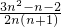 .
.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案