增区间为[3,+∞),减区间为(-∞,-1]
分析:先根据函数的解析式求得函数的定义域,进而根据函数y=x
2-2x-3的单调区间求得函数f(x)的单调区间.
解答:要使根号有意义需x
2-2x-3≥0
解得x≥3或x≤-1
故函数的定义域为{x|x≥3或x≤-1}
对于函数y=x
2-2x-3=(x-1)
2-4
当x≥1时函数单调性增,x≤1时,函数单调减
∴f(x)=
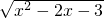
当x≥3时单调增,当x≤-1时函数单调减
故函数的增区间为[3,+∞),减区间为(-∞,-1]
故答案为:增区间为[3,+∞),减区间为(-∞,-1]
点评:本题主要考查了函数单调性及其区间.解题的时候一定要注意函数的定义域问题.

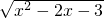 的单调区间为 ________.
的单调区间为 ________.