
分析 利用“倍值区间”的意义,只要方程f(x)=2x在定义域内存在两个不同实数根即可得出.
解答 解:①假设函数f(x)存在“倍值区间”[a,b],由于x≥0,∴函数f(x)在[a,b]上单调递增,令x2=2x,解得x=0,2,∴[0,2]是函数f(x)的“倍值区间”;
同理可得:②存在“倍值区间”[1,2];③不存在“倍值区间”.
④假设函数f(x)存在“倍值区间”[a,b],令$lo{g}_{a}({a}^{x}-\frac{1}{8})$=2x,化为8(ax)2-8ax+1=0,∵△=64-32=32>0,解得ax=$\frac{2±\sqrt{2}}{4}$,因此x有两个不同的实数值满足方程.∴假设正确.
综上可得:只有①②④存在“倍值区间”.
故答案为:①②④.
点评 本题考查了系新定义“倍值区间”、方程的解法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=1,g(x)=x0 | B. | f(x)=1,g(x)=$\frac{x}{x}$ | ||
| C. | f(x)=$\frac{(x+3)^{2}}{x+3}$,g(x)=(x+3)(x+3)0 | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x,x>0}\\{-x,x<0}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
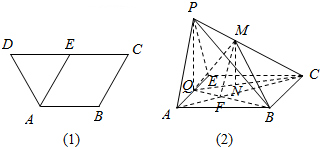 在等腰梯形ABCD中,AB∥CD,AB=BC=AD=2,CD=4,E为边DC的中点.如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.
在等腰梯形ABCD中,AB∥CD,AB=BC=AD=2,CD=4,E为边DC的中点.如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
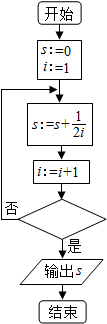
| A. | i>5 | B. | i<5 | C. | i>10 | D. | i<10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com