
设函数 的图像在
的图像在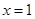 处取得极值4.
处取得极值4.
(1)求函数 的单调区间;
的单调区间;
(2)对于函数 ,若存在两个不等正数
,若存在两个不等正数
 ,当
,当 时,函数
时,函数 的值域是
的值域是 ,则把区间
,则把区间 叫函数
叫函数 的“正保值区间”.问函数
的“正保值区间”.问函数 是否存在“正保值区间”,若存在,求出所有的“正保值区间”;若不存在,请说明理由.
是否存在“正保值区间”,若存在,求出所有的“正保值区间”;若不存在,请说明理由.
(1)递增区间是 和
和 ,递减区间是
,递减区间是 ;(2)不存在.
;(2)不存在.
【解析】
试题分析:(1)求导,利用极值点的坐标列出方程组,解出 ,确定函数解析式,再求导,求单调区间;(2)先假设存在“正保值区间”
,确定函数解析式,再求导,求单调区间;(2)先假设存在“正保值区间” ,通过已知条件验证是否符合题意,排除不符合题意得情况.
,通过已知条件验证是否符合题意,排除不符合题意得情况.
试题解析:(1) ,
1分
,
1分
依题意则有: ,即
,即 解得
解得 v
3分
v
3分
∴ .令
.令 ,
,
由 解得
解得 或
或 ,v
5分
,v
5分
所以函数 的递增区间是
的递增区间是 和
和 ,递减区间是
,递减区间是 6分
6分
(2)设函数 的“正保值区间”是
的“正保值区间”是 ,因为
,因为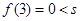 ,
,
故极值点 不在区间
不在区间 上;
上;
①若极值点 在区间
在区间 ,此时
,此时 ,在此区间上
,在此区间上 的最大值是
的最大值是 4,不可能等于
4,不可能等于 ;故在区间
;故在区间 上没有极值点;
8分
上没有极值点;
8分
②若 在
在 上单调递增,即
上单调递增,即 或
或 ,
,
则 ,即
,即 ,解得
,解得 或
或 不符合要求; 10分
不符合要求; 10分
③若 在
在 上单调减,即1<s<t<3,则
上单调减,即1<s<t<3,则 ,
,
两式相减并除 得:
得: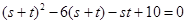 , ①
, ①
两式相除可得 ,即
,即 ,
,
整理并除以 得:
得: , ②
, ②
由①、②可得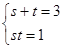 ,即
,即 是方程
是方程 的两根,
的两根,
即存在 ,
, 不合要求.
12分
不合要求.
12分
综上可得不存在满足条件的s、t,即函数 不存在“正保值区间”。 13分
不存在“正保值区间”。 13分
考点:1.求函数的极值;2.求最值;3.求单调区间.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源:2013-2014学年江西省七校高三上学期第一次联考文科数学试卷(解析版) 题型:解答题
设函数 。
。
(Ⅰ)若 时,函数
时,函数 取得极值,求函数
取得极值,求函数 的图像在
的图像在 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在区间
在区间 内不单调,求实数
内不单调,求实数 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2013届湖南省上学期高二期中考试理科数学试卷(解析版) 题型:解答题
设函数 的图像与y轴交点为
的图像与y轴交点为 ,且曲线在
,且曲线在 点处的切线方程为
点处的切线方程为 ,若函数在
,若函数在 处取得极值为
处取得极值为 .(1)求函数解析式;(2)确定函数的单调递增区间;(3)证明:当
.(1)求函数解析式;(2)确定函数的单调递增区间;(3)证明:当 (14分)
(14分)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三第二次联考数学文卷 题型:解答题
设函数 。
。
(1)若 时,函数
时,函数 取得极值,求函数
取得极值,求函数 的图像在
的图像在 处的切线方程;
处的切线方程;
(2)若函数 在区间
在区间 内不单调,求实数
内不单调,求实数 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com