
| a |
| x |
| n |
 |
| i+1 |
| i |
| i+1 |
| x-a |
| x2 |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 3 |
| 2 |
| n+1 |
| n |
| 2 |
| 1 |
| 3 |
| 2 |
| n+1 |
| n |
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
| n |
 |
| i=1 |
| i |
| i+1 |
| x-a |
| x2 |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 3 |
| 2 |
| n+1 |
| n |
| 2 |
| 1 |
| 2 | ||
|
| 1 |
| 2 |
| 3 |
| 2 |
| 2 | ||
|
| 2 |
| 3 |
| n+1 |
| n |
| n |
| n+1 |
| 2 |
| 1 |
| 3 |
| 2 |
| n+1 |
| n |
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
| n |
 |
| i=1 |
| i |
| i+1 |


科目:高中数学 来源: 题型:
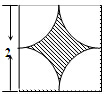 如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )
如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )A、
| ||
B、
| ||
C、1-
| ||
D、1-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
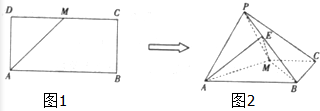 如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=
如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| C |
| 2 |
| n |
| 3 |
| sin2A |
| 1 |
| cos2A |
| 1 |
| cosB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| ρ2 |
| cos2θ |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
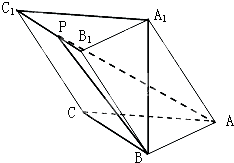 在三棱柱ABC-A1B1C1中,已知AB=BC=2,∠ABC=90°,点A1在底面ABC的投影为B,且A1B=2
在三棱柱ABC-A1B1C1中,已知AB=BC=2,∠ABC=90°,点A1在底面ABC的投影为B,且A1B=2| 3 |
| 29 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an |
| 2n |
| an |
| 2n |
| 1 |
| bnbn+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|

查看答案和解析>>
科目:高中数学 来源: 题型:
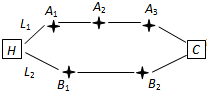 家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为
家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
| 路线 | 距离(公里) | 行驶费用(元/公里) | 遇红灯时 费用(元/次) |
| L1 | 20 | 1.5 | 1.5 |
| L2 | 30 | 1 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com