
 M(t,f(t))处的切线为l,l与y轴和直线y=1分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为
M(t,f(t))处的切线为l,l与y轴和直线y=1分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为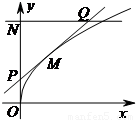




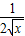 ,根据导数的几何意义先写出过点M的切线方程为y-
,根据导数的几何意义先写出过点M的切线方程为y-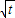 =
=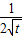 (x-t),进而可得面积S=
(x-t),进而可得面积S=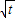 -t+
-t+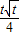 ,令g(t)为一个新的函数,要使△PQN的面积为b时的点M恰好有两个即g(t)在(0,1)上与y=b有两个交点,通过g′(t)研究函数函数g(t)在(0,1)上的单调性,结合函数的图象进行求解;
,令g(t)为一个新的函数,要使△PQN的面积为b时的点M恰好有两个即g(t)在(0,1)上与y=b有两个交点,通过g′(t)研究函数函数g(t)在(0,1)上的单调性,结合函数的图象进行求解;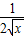 ,由题意可得M(t,
,由题意可得M(t,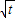 ),
),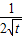
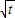 =
=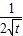 (x-t)
(x-t)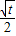 ),N(0,1),Q(2
),N(0,1),Q(2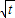 -t,1),
-t,1), PN•NQ=
PN•NQ= (2
(2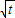 -t)(1-
-t)(1-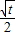 )=
)=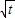 -t+
-t+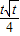 ,
,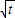 -t+
-t+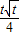 (0<t<1)
(0<t<1)
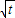 +
+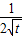 -1=
-1=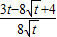 =
=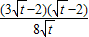 ,
, )单调递增,在[
)单调递增,在[ ,1)单调递减,
,1)单调递减, ,g(
,g( )=
)=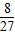 ,
, <b<
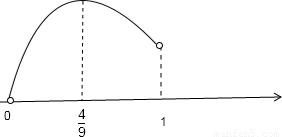
<b<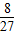 ,
,


科目:高中数学 来源: 题型:
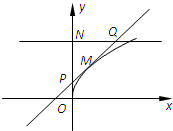 如图为函数f(x)=
如图为函数f(x)=| x |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 如图为函数
如图为函数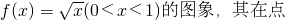 M(t,f(t))处的切线为l,l与y轴和直线y=1分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为
M(t,f(t))处的切线为l,l与y轴和直线y=1分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为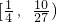
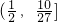
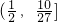
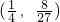
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都四中高三(上)期中数学试卷(文科)(解析版) 题型:选择题
 M(t,f(t))处的切线为l,l与y轴和直线y=1分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为
M(t,f(t))处的切线为l,l与y轴和直线y=1分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为



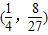
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都四中高三(上)期中数学试卷(文科)(解析版) 题型:选择题
 M(t,f(t))处的切线为l,l与y轴和直线y=1分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为
M(t,f(t))处的切线为l,l与y轴和直线y=1分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com