
设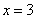 是函数
是函数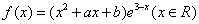 的一个极值点.
的一个极值点.
(1)求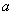 与
与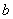 的关系式(用
的关系式(用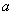 表示
表示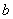 ),并求
),并求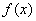 的单调区间;
的单调区间;
(2)设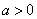 ,
,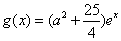 .若存在
.若存在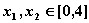 使得
使得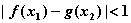 成立,求
成立,求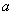 的取值范围.
的取值范围.
解:(Ⅰ)f `(x)=-[x2+(a-2)x+b-a ]e3-x,
由f `(3)=0,得 -[32+(a-2)3+b-a ]e3-3=0,即得b=-3-2a,
则 f `(x)=[x2+(a-2)x-3-2a-a ]e3-x
=-[x2+(a-2)x-3-3a ]e3-x=-(x-3)(x+a+1)e3-x.
令f `(x)=0,得x1=3或x2=-a-1,由于x=3是极值点,
所以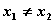 ,那么a≠-4.
,那么a≠-4.
当a<-4时,x2>3=x1,则
在区间(-∞,3)上,f `(x)<0, f (x)为减函数;
在区间(3,—a—1)上,f `(x)>0,f (x)为增函数;
在区间(—a—1,+∞)上,f `(x)<0,f (x)为减函数.
当a>-4时,x2<3=x1,则
在区间(-∞,—a—1)上,f `(x)<0, f (x)为减函数;
在区间(—a—1,3)上,f (x)>0,f (x)为增函数;
在区间(3,+∞)上,f `(x)<0,f (x)为减函数.
(Ⅱ)由(Ⅰ)知,当a>0时,f (x)在区间(0,3)上的单调递增,在区间(3,4)上单调递减,那么f (x)在区间[0,4]上的值域是[min{f (0),f (4) },f (3)],
而f (0)=-(2a+3)e3<0,f (4)=(2a+13)e-1>0,f (3)=a+6,
那么f (x)在区间[0,4]上的值域是[-(2a+3)e3,a+6].
又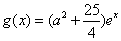 在区间[0,4]上是增函数,
在区间[0,4]上是增函数,
且它在区间[0,4]上的值域是[a2+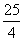 ,(a2+
,(a2+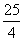 )e4],
)e4],
由于(a2+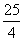 )-(a+6)=a2-a+
)-(a+6)=a2-a+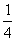 =(
=( )2≥0,所以只须仅须
)2≥0,所以只须仅须
(a2+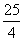 )-(a+6)<1且a>0,解得0<a<
)-(a+6)<1且a>0,解得0<a<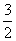 .
.
故a的取值范围是(0,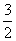 ).
).


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com