
已知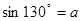 ,则
,则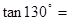
 .
.
科目:高中数学 来源: 题型:填空题
设函数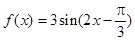 的图象为
的图象为 ,给出下列命题:
,给出下列命题:
①图象 关于直线
关于直线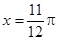 对称; ②函数
对称; ②函数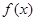 在区间
在区间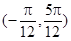 内是增函数;
内是增函数;
③函数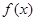 是奇函数; ④图象
是奇函数; ④图象 关于点
关于点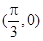 对称. ⑤
对称. ⑤ 的周期为
的周期为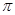
其中,正确命题的编号是 .(写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函数 的图像恰好经过
的图像恰好经过 个格点,则称函数
个格点,则称函数 为
为 阶格点函数.已知函数:①
阶格点函数.已知函数:① ;②
;② ;③
;③ ;④
;④ .其中为一阶格点函数的序号为
.其中为一阶格点函数的序号为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com