
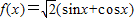 ,给出下列四个命题:
,给出下列四个命题: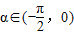 ,使
,使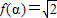 ;
; 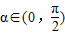 ,使f(x-α)=f(x+α)恒成立;
,使f(x-α)=f(x+α)恒成立;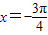 对称;
对称;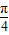 就能得到y=-2cosx的图象
就能得到y=-2cosx的图象 =2sin(x+
=2sin(x+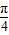 )
)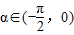 时,α+
时,α+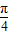 ∈(-
∈(-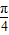 ,
,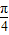 ),此时f(α)∈(-
),此时f(α)∈(-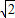 ,
,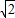 ),故①错误;
),故①错误; +kπ,k∈Z,使函数f(x+ϕ)的图象关于坐标原点成中心对称,故③正确;
+kπ,k∈Z,使函数f(x+ϕ)的图象关于坐标原点成中心对称,故③正确;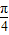 +kπ,k∈Z,当k=-1时,
+kπ,k∈Z,当k=-1时,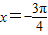 ,故④正确;
,故④正确;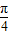 后得到y=2sin(x+
后得到y=2sin(x+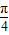 +
+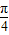 )=2sin(x+
)=2sin(x+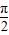 )=2cosx的图象,故⑤错误;
)=2cosx的图象,故⑤错误;

科目:高中数学 来源: 题型:
对于函数![]() ,给出下列四个命题:①
,给出下列四个命题:①![]() 是增函数,无极值;②
是增函数,无极值;②![]() 是减函数,有极值;③
是减函数,有极值;③![]() 在区间
在区间![]() 及
及![]() 上是增函数;④
上是增函数;④![]() 有极大值为
有极大值为![]() ,极小值
,极小值![]() ;其中正确命题的个数为( )
;其中正确命题的个数为( )
(A)![]() (B)
(B)![]()
![]() (C)
(C)![]() (D)
(D)![]()
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省高三第十次模拟考试理科数学试卷(解析版) 题型:选择题
对于函数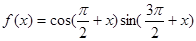 ,给出下列四个结论:①函数
,给出下列四个结论:①函数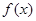 的最小正周期为
的最小正周期为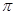 ;②若
;②若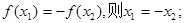 ③
③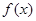 的图象关于直线
的图象关于直线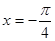 对称;④
对称;④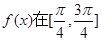 上是减函数,其中正确结论的个数为 ( )
上是减函数,其中正确结论的个数为 ( )
A.2 B.4 C.1 D.3
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高三上学期联考理科数学 题型:填空题
对于函数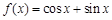 ,给出下列四个命题:
,给出下列四个命题:
①存在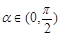 ,使
,使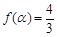 ;
;
②存在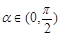 ,使
,使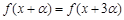 恒成立;
恒成立;
③存在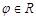 ,使函数
,使函数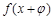 的图象关于y轴对称;
的图象关于y轴对称;
④函数f(x)的图象关于点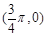 对称.
对称.
其中正确命题的序号是
查看答案和解析>>
科目:高中数学 来源:山东省枣庄市2010届高三年级调研考试数学(理科)试题 题型:选择题
对于函数 ,给出下列四个结论:①函数
,给出下列四个结论:①函数 的最小正周期为
的最小正周期为 ;②若
;②若 ③
③ 的图象关于直线
的图象关于直线 对称;④
对称;④ 上是减函数,其中正确结论的个数为 ( )
上是减函数,其中正确结论的个数为 ( )
A.2 B.4 C.1 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com