
图
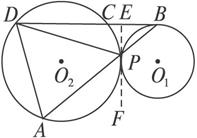
求证:AD2+BC·BD=AB2.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
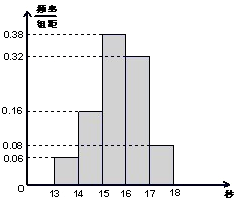 某班50名学生在一次百米测试中,成绩全部介于13~18秒之间,将测试结果分成五组:第一组[13,14),经二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图,若成绩大于或等于14秒且小于16秒认为良好.
某班50名学生在一次百米测试中,成绩全部介于13~18秒之间,将测试结果分成五组:第一组[13,14),经二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图,若成绩大于或等于14秒且小于16秒认为良好.查看答案和解析>>
科目:高中数学 来源:2010年北京市崇文区高三下学期一模数学(文)测试 题型:解答题
(本小题共13分)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了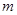 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为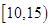 ,
,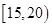 ,
,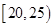 ,
,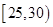 ,
,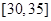 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在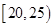 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求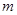 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
人不在同一组的概率是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题共13分)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了![]() 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
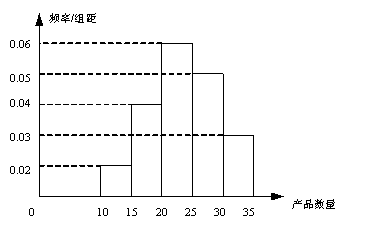
,![]() ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在![]() 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求![]() ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
 人不在同一组的概率是多少?
人不在同一组的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题共13分)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了![]() 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
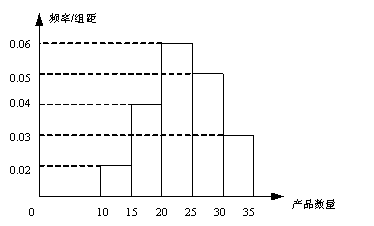
,![]() ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在![]() 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求![]() ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
 人不在同一组的概率是多少?
人不在同一组的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com