
已知函数 的图象在点
的图象在点 (e为自然对数的底数)处取得极值-1.
(e为自然对数的底数)处取得极值-1.
(1)求实数 的值;
的值;
(2)若不等式 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)-2;(2)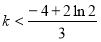
【解析】
试题分析:(1)因为函数 的图象在点
的图象在点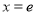 (e为自然对数的底数)处取得极值-1,所以
(e为自然对数的底数)处取得极值-1,所以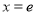 时导函数的值为零.即可求出
时导函数的值为零.即可求出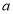 的值.
的值.
(2)因为不等式 对任意
对任意 恒成立,所以写出等价的不等式,从而转化为求函数的在
恒成立,所以写出等价的不等式,从而转化为求函数的在 时的最小值的问题.所以通过对函数的求导,观察发现函数的单调性即可得到函数的在
时的最小值的问题.所以通过对函数的求导,观察发现函数的单调性即可得到函数的在 范围的最小值.从而得到结论.
范围的最小值.从而得到结论.
试题解析:(1)【解析】
因为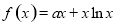 ,所以
,所以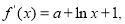
因为函数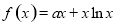 的图像在点
的图像在点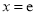 处取得极值,
处取得极值,
所以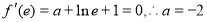 . 4分
. 4分
(2)【解析】
由(1)知,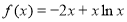 ,
,
所以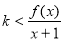 对任意
对任意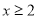 恒成立,即
恒成立,即 对任意
对任意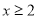 恒成立.
恒成立.
令 ,则,
,则,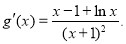
因为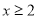 ,所以
,所以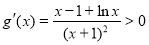 ,
,
所以函数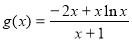 在
在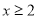 上为增函数,
上为增函数,
则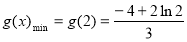 ,
,
所以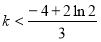 . 12分
. 12分
考点:1.函数的极值.2.函数的最值问题.3.不等式的恒成立问题.4.数形结合的思想.


科目:高中数学 来源:2015届浙江省台州市高二第一学期期末数学试卷(解析版) 题型:选择题
右图是边长相等的两个正方形.给定下列三个命题:

①存在三棱柱,其正视图、侧视图如右图;
②存在四棱柱,其正视图、侧视图如右图;
③存在圆柱,其正视图、侧视图如右图.
其中真命题的个数是
A. 3 B.2 C.1 D.0
查看答案和解析>>
科目:高中数学 来源:2015届河南郑州高二上学期期末考试理科数学试卷(解析版) 题型:选择题
抛物线 的焦点F恰好是双曲线
的焦点F恰好是双曲线 的右焦点,且它们的交点的连线过点F,则双曲线的离心率为 ( )
的右焦点,且它们的交点的连线过点F,则双曲线的离心率为 ( )
A.  B.
B.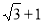 C. 3 D.
C. 3 D.
查看答案和解析>>
科目:高中数学 来源:2015届河南郑州高二上学期期末考试文科数学试卷(解析版) 题型:解答题
已知命题 :“不等式
:“不等式 对任意
对任意 恒成立”,命题
恒成立”,命题 :“
:“ 表示焦点在x轴上的椭圆”,若
表示焦点在x轴上的椭圆”,若 为真命题,
为真命题,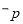 为真,求实数
为真,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届河南郑州高二上学期期末考试文科数学试卷(解析版) 题型:选择题
设等差数列 的公差
的公差 ,
, ,若
,若 是
是 与
与 的等比中项,则
的等比中项,则 =( )
=( )
A. 3或6 B.3 或9 C. 3 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com