

 时,求y=T4(x)的解析式;
时,求y=T4(x)的解析式; 时(i∈N*,1≤i≤15),都有
时(i∈N*,1≤i≤15),都有 恒成立.
恒成立. 大小,然后把x2代入已知函数解析式中可求y=T(x2),对已知所给函数解析式直接进行平方可求y=(T(x))2的解析式;
大小,然后把x2代入已知函数解析式中可求y=T(x2),对已知所给函数解析式直接进行平方可求y=(T(x))2的解析式;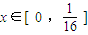 时,根据函数定义域的要求可知,
时,根据函数定义域的要求可知,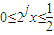 ,结合此规律寻求函数的递推规律可求故有
,结合此规律寻求函数的递推规律可求故有 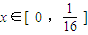 时,有T4(x)=16x,根据命题的结论可得,
时,有T4(x)=16x,根据命题的结论可得, ,代入可求,同理归纳可求
,代入可求,同理归纳可求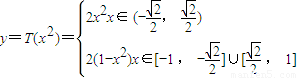
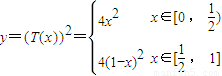 …4分
…4分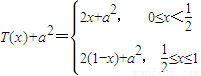 ,
,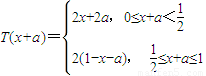 …6分
…6分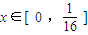 时,对于任意的正整数j∈N*,1≤j≤3,
时,对于任意的正整数j∈N*,1≤j≤3,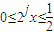 ,故有
,故有 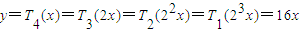 .…13分
.…13分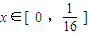 时,有T4(x)=16x,根据命题的结论可得,
时,有T4(x)=16x,根据命题的结论可得,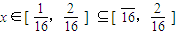 时,
时,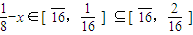 ,
, ,
,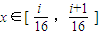 (i∈N,0≤i≤15)时,
(i∈N,0≤i≤15)时,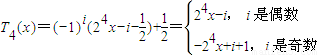 …15分
…15分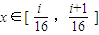 时,解方程T4(x)=kx得,
时,解方程T4(x)=kx得,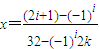
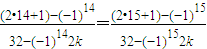 解得
解得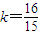
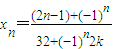 (n∈N*,1≤n≤15)…17分
(n∈N*,1≤n≤15)…17分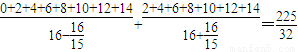 .…18分.
.…18分.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2x+1-n |
| x2+x+1 |
| lim |
| n→∞ |
| ||
| Cn |
| 1 |
| C1 |
| 1 |
| C2 |
| 1 |
| Cn |
| m |
| 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
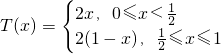
 x))和y=sin(
x))和y=sin( T(x))的解析式;
T(x))的解析式; ]时,求y=Tn(x)的解析式;
]时,求y=Tn(x)的解析式;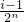 ,
,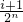 ](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(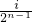 -x)恒成立.
-x)恒成立.查看答案和解析>>
科目:高中数学 来源:2013年上海市浦东新区高考数学一模试卷(理科)(解析版) 题型:解答题
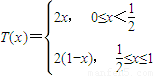
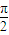 x))和y=sin(
x))和y=sin(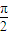 T(x))的解析式;
T(x))的解析式;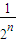 ]时,求y=Tn(x)的解析式;
]时,求y=Tn(x)的解析式;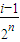 ,
,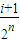 ](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(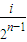 -x)恒成立.
-x)恒成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com