
设 则
则 ( )
( )
A.都不大于 |
B.都不小于 |
C.至少有一个不大于 |
D.至少有一个不小于 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
给出30个数:1,2,4,7,……,其规律是:第1个数是1,第2个数比第1个数大1, 第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示)
(I)请在图中判断框内(1)处和执行框中的(2)处填上合适的语句,使之能完成该题算法功能;
(II)根据程序框图写出程序.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
| A.假设三内角都不大于60度 |
| B.假设三内角都大于60度 |
| C.假设三内危至多有一个大于60度 |
| D.假设三内角至多有两个大于60度 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
图1,2,3,4分别包含1,5,13和25个互不重叠的单位正方形,按同样的方式构造图形,则第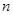 个图包含______个互不重叠的单位正方形。
个图包含______个互不重叠的单位正方形。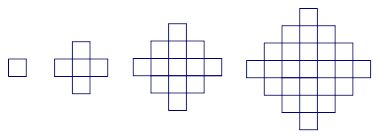
图1 图2 图3 图4
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
法国数学家费马观察到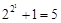 ,
, ,
, ,
, 都是质数,于是他提出猜想:任何形如
都是质数,于是他提出猜想:任何形如 N*)的数都是质数,这就是著名的费马猜想. 半个世纪之后,善于发现的欧拉发现第5个费马数
N*)的数都是质数,这就是著名的费马猜想. 半个世纪之后,善于发现的欧拉发现第5个费马数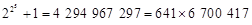 不是质数,从而推翻了费马猜想,这一案例说明( )
不是质数,从而推翻了费马猜想,这一案例说明( )
| A.归纳推理,结果一定不正确 | B.归纳推理,结果不一定正确 |
| C.类比推理,结果一定不正确 | D.类比推理,结果不一定正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若a,b∈R,则a-b=0⇒a=b”,类比推出“若a,b∈C,则a-b=0⇒a=b”;
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”,类比推出,“若a,b,c,d∈Q,则a+b =c+d
=c+d ⇒a=c,b=d”;
⇒a=c,b=d”;
③“若a,b∈R,则a-b>0⇒a>b”,类比推出“若a,b∈C,则a-b>0⇒a>b”;
④“若x∈R,则|x|<1⇒-1<x<1”,类比推出“若z∈C,则|z|<1⇒-1<z<1”.
其中类比正确的为( )
| A.①② | B.①④ | C.①②③ | D.②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com