
(本小题满分10分)已知函数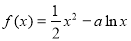

(1)若函数 在
在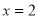 处的切线方程为
处的切线方程为 ,求
,求 的值;
的值;
(2)讨论方程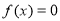 解的个数,并说明理由。
解的个数,并说明理由。
(1)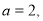
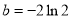 ,(2)当
,(2)当 时,方程有惟一解;当
时,方程有惟一解;当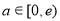 时,方程无解;当
时,方程无解;当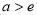 时方程有两解.
时方程有两解.
【解析】
试题分析:第一步函数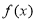 在
在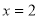 处的切线方程为
处的切线方程为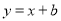 ,切线斜率为1,由于
,切线斜率为1,由于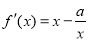 ,则
,则
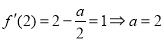 ,而
,而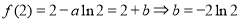 ,第二步由于函数定义域为
,第二步由于函数定义域为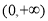 ,
,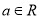 ,当
,当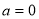 时,
时,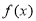 在定义域
在定义域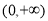 上恒大于
上恒大于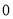 ,此时方程无解;当
,此时方程无解;当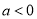 时,
时,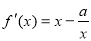
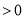 ,函数
,函数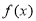 在定义域
在定义域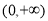 上为增函数,因为
上为增函数,因为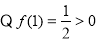 ,
,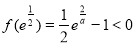 ,则
,则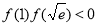 ,函数
,函数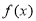 有唯一一个零点,所以方程有惟一解;当
有唯一一个零点,所以方程有惟一解;当 时,
时, ,
,
函数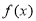 在
在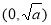 上是减函数,在
上是减函数,在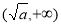 内为增函数,当
内为增函数,当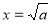 时,有极小值即为最小值
时,有极小值即为最小值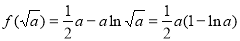 ,最后根据最小值分大于零、等于零、小于零三种情形对应方程根的个数实施讨论,给出各种情形的答案即可;
,最后根据最小值分大于零、等于零、小于零三种情形对应方程根的个数实施讨论,给出各种情形的答案即可;
试题解析:(1)因为: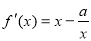
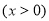 ,又
,又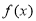 在
在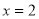 处的切线方程为
处的切线方程为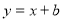
所以 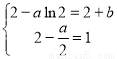 解得:
解得: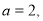
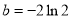
(2)当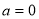 时,
时,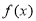 在定义域
在定义域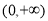 上恒大于
上恒大于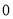 ,此时方程无解;当
,此时方程无解;当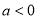 时,
时,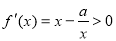 在
在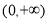 上恒成立, 所以
上恒成立, 所以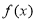 在定义域
在定义域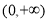 上为增函数。
上为增函数。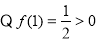 ,
,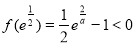 ,所以方程有惟一解。
,所以方程有惟一解。
当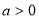 时,
时,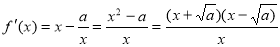 ,因为当
,因为当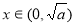 时,
时,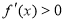 ,
,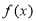 在
在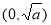 内为减函数;当
内为减函数;当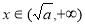 时,
时,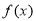 在
在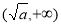 内为增函数。所以当
内为增函数。所以当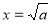 时,有极小值即为最小值
时,有极小值即为最小值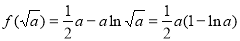
当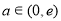 时,
时,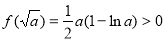 ,此方程无解;
,此方程无解;
当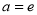 时,
时,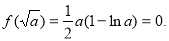 此方程有惟一解
此方程有惟一解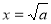 。
。
当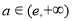 时,
时,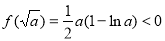 ,因为
,因为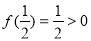 且
且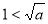 ,所以方程
,所以方程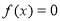 在区间
在区间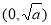 上有惟一解, 又因为当
上有惟一解, 又因为当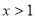 时,
时,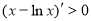 ,所以
,所以 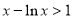 ,所以
,所以 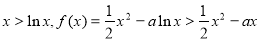 ,因为
,因为 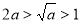 ,所以
,所以 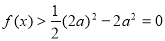 所以 方程
所以 方程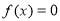 在区间
在区间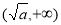 上有惟一解。所以方程
上有惟一解。所以方程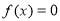 在区间
在区间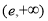 上有两解。
上有两解。
综上所述:当 时,方程有惟一解;当
时,方程有惟一解;当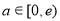 时,方程无解;当
时,方程无解;当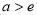 时方程有两解。
时方程有两解。
考点:1.导数的几何意义;2.利用导数研究函数的单调性、极值、函数的零点;3.导数的应用;


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源:2014-2015学年北京市东城区高三上学期期末教学统一检测理科数学试卷(解析版) 题型:选择题
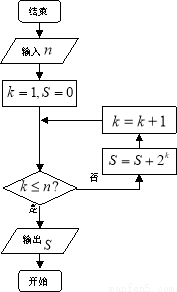
当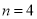 时,执行如图所示的程序框图,输出的
时,执行如图所示的程序框图,输出的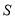 值为
值为
(A) (B)
(B)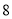 (C)
(C)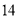 (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
如图所示是正方体的平面展开图.在这个正方体中,①BM与ED平行;②CN与BE是异面直线;③CN与BM成60°角;④DM与BN是异面直线.以上四个命题中,正确命题的序号是( )

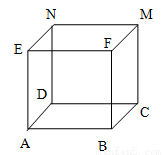
A.①②③ B.②④ C.③④ D.②③④
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)若极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的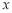 轴的正半轴重合.
轴的正半轴重合.
直线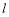 的参数方程是
的参数方程是 (
(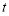 为参数),曲线
为参数),曲线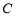 的极坐标方程为
的极坐标方程为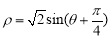 .
.
(1)求曲线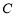 的直角坐标方程;
的直角坐标方程;
(2)设直线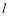 与曲线
与曲线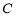 相交于
相交于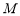 ,
, 两点,求M,N两点间的距离.
两点,求M,N两点间的距离.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二上学期期末考试文科数学试卷(解析版) 题型:选择题
已知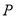 是抛物线
是抛物线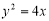 上的一个动点,
上的一个动点,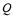 是圆
是圆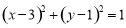 上的一个动点,
上的一个动点,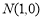 是一个定点,则
是一个定点,则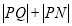 的最小值为( )
的最小值为( )
A.3 B.4 C.5 D.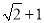
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省高二文特班上学期第二次月考数学试卷(解析版) 题型:解答题
教室内有5个学生,分别佩戴1号到5号的校徽,任选3人记录他们的校徽号码。
(1)求最小号码为2的概率;
(2)求三个号码中至多有一个偶数的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com