Question

15．某班决定举行联欢会迎接元旦，小明负责游戏环节，他设计了一个“击球猜谜”的游戏，需要先在长为6米的绳子上挂上两个气球．
（1）若这两个小球挂在绳子的6等分点处，求两个气球相邻的概率；（两个气球不能挂在同一个等分点）．
（2）若其中一个气球挂在绳子的左起第一个三等分点处，求两个气球之间的距离不小于1米的概率．

Answer 1

分析 （1）设绳子的5个6等分点的标号为1，2，3，4，5，利用列举法结合古典概型的概率公式进行求解即可．
（2）求出满足两个气球之间的距离不小于1米条件，结合几何概型的概率公式进行求解即可．

解答 解：（1）令两个气球相邻的事件为A，
绳子的5个6等分点的标号为1，2，3，4，5，
这两个小球挂在绳子的6等分点处所有的可能有（1，2），（1，3），（1，4），（1，5），（2，3），（2，4），（2，5），（3，4），（3，5），（4，5）共有10种，
则两个气球相邻的有（1，2），（2，3），（3，4），（4，5）共有4种，
则两个气球相邻的概率为P（A）=$\frac{4}{10}=\frac{2}{5}$．
（2）设两个气球之间的距离不小于1米的事件为B．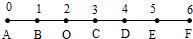
如图其中一个气球挂在绳子的左起第一个三等分点处O，令BO=CO=1，
若两个气球之间的距离不小于1米，
则另外一个球应该挂着AB之间或者CF之间，
∵|AB|=1，|CF|=3，
∴|AB|+|CF|=1+3=4，
则两个气球之间的距离不小于1米的概率P（B）=$\frac{4}{6}=\frac{2}{3}$．

点评 本题主要考查古典概型和几何概型的概率的计算，利用列举法是解决古典概型的常用方法．