
分析 (1)直接利用有理指数幂的运算法则化简求解即可.
(2)利用对数的运算法则化简求解即可.
解答 解:(1)${0.064^{-\frac{1}{3}}}-{({-\frac{1}{8}})^0}+{16^{\frac{3}{4}}}+{0.25^{\frac{1}{2}}}$
=0.4-1-1+23+0.5
=2.5-1+8+0.5
=10;
(2)${2^{2+{{log}_2}5}}-{2^{{{log}_2}3{{log}_3}5}}$
=${2}^{2+{log}_{2}5}-{2}^{{log}_{2}{3}^{{log}_{3}5}}$
=4×5-5=15.
点评 本题考查指数与对数的运算法则的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | (-6,7) | B. | (-15,1) | C. | (-14,2) | D. | (-8,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
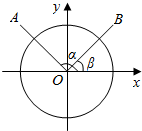 如图,以ox为始边作角α与β(0<β<α<π),它们的终边 分别与单位圆相交于点A、B.已知点A的坐标为(-$\frac{3}{5}$,$\frac{4}{5}$).
如图,以ox为始边作角α与β(0<β<α<π),它们的终边 分别与单位圆相交于点A、B.已知点A的坐标为(-$\frac{3}{5}$,$\frac{4}{5}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2015年我国将加快阶梯水价的推行,原则是“保基本、建机制、促节约”,其中“保基本是指保证至少80%的居民用户用水价格不变,为响应国家政策,制定合理的阶梯用水价格,某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研,抽取的数据的茎叶图如图(单位:吨).
2015年我国将加快阶梯水价的推行,原则是“保基本、建机制、促节约”,其中“保基本是指保证至少80%的居民用户用水价格不变,为响应国家政策,制定合理的阶梯用水价格,某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研,抽取的数据的茎叶图如图(单位:吨).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com