
分析 由x2+4x=0,解得A={0,-4}.由x2+2ax+a(a-2)=0,可得:△=8a.对a分类讨论,利用集合之间的关系即可得出.
解答 解:由x2+4x=0,解得x=0或-4.∴A={0,-4}.
由x2+2ax+a(a-2)=0,可得:△=4a2-4a(a-2)=8a.
①a<0时,B=∅,满足B⊆A;
②a=0时,B={0},满足B⊆A;
③a>0时,∵B⊆A,则B=A={0,-4},∴$\left\{\begin{array}{l}{0-4=-2a}\\{0×(-4)=a(a-2)}\end{array}\right.$,解得a=2.
综上可得:a≤0或a=2.
∴满足B⊆A的实数a的值组成的集合是(-∞,0]∪{2}.
点评 本题考查了集合之间的关系、方程的解法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
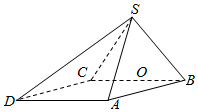 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知:∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC,直线SD与平面ABCD所成角的正弦值为$\frac{\sqrt{11}}{11}$.O为BC的中点.
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知:∠ABC=45°,AB=2,BC=2$\sqrt{2}$,SB=SC,直线SD与平面ABCD所成角的正弦值为$\frac{\sqrt{11}}{11}$.O为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{11}{4}$-ln2] | B. | (-∞,$\frac{5}{4}$-ln2] | C. | (-∞,$\frac{5}{2}$-e${\;}^{\frac{1}{2}}$] | D. | (-∞,$\frac{15}{4}$-e${\;}^{\frac{1}{4}}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | [2,$\frac{23}{8}$] | C. | [$\frac{5}{16}$,$\frac{9}{16}$] | D. | [$\frac{27}{16}$,$\frac{9}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com