
| A. | (-∞,$\frac{11}{4}$-ln2] | B. | (-∞,$\frac{5}{4}$-ln2] | C. | (-∞,$\frac{5}{2}$-e${\;}^{\frac{1}{2}}$] | D. | (-∞,$\frac{15}{4}$-e${\;}^{\frac{1}{4}}$] |
分析 设f(a)=f(b)=f(c)=t,作出函数的图象,结合图象判断0<t<1,分别用t表示a,b,c,然后构造函数,求函数的导数,利用导数研究函数的极值和最值即可求a+3b+c的取值范围.
解答 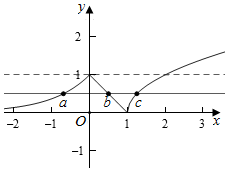 解:先作出函数f(x)的图象如图:
解:先作出函数f(x)的图象如图:
∵a<b<c.f(a)=f(b)=f(c),
设f(a)=f(b)=f(c)=t,
则0<t<1,
则由f(a)=ea=t,得a=lnt,
由f(b)=1-b=t,得b=1-t,
由f(c)=$\sqrt{c-1}$=t,得c=t2+1,
则a+3b+c=lnt+3(1-t)+t2+1=t2-3t+lnt+4
设g(t)=t2-3t+lnt+4,0<t<1,
函数的导数g′(t)=2t-3+$\frac{1}{t}$=$\frac{2{t}^{2}-3t+1}{t}$=$\frac{(2t-1)(t-1)}{t}$,
由g′(t)=0得t=$\frac{1}{2}$,
当0<t<$\frac{1}{2}$时,g′(t)>0,此时函数递增,
当$\frac{1}{2}$<t<1时,g′(t)<0,此时函数递减,
即当t=$\frac{1}{2}$时,函数g(t)取得极大值同时也是最大值g($\frac{1}{2}$)=$\frac{1}{4}$-$\frac{3}{2}$+ln$\frac{1}{2}$+4=$\frac{11}{4}$-ln2,
∴g(t)≤$\frac{11}{4}$-ln2,
即a+3b+c的取值范围是(-∞,$\frac{11}{4}$-ln2],
故选:A.
点评 本题考查分段函数的应用,设f(a)=f(b)=f(c)=t,利用t表示a,b,c,构造函数,求函数的导数,利用导数研究函数的最值是解决本题的关键.综合性较强,有一定的难度.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{2}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{4}$,0) | D. | ($\frac{π}{6}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
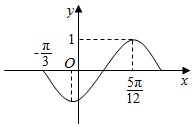 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的几何体ABCEF中,BF⊥平面ABC,D为线段BC的中点,CE∥BF,∠BAC=90°,且AB=AC=BF=2CE.
如图所示的几何体ABCEF中,BF⊥平面ABC,D为线段BC的中点,CE∥BF,∠BAC=90°,且AB=AC=BF=2CE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{3}$) | B. | ($\frac{2}{3}$,+∞) | C. | (0,$\frac{1}{3}$)∪($\frac{1}{3}$,$\frac{2}{3}$) | D. | ($\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com