
已知函数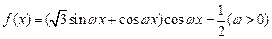 最小正周期为
最小正周期为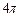
(1)求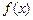 的单调递增区间
的单调递增区间
(2)在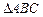 中,角
中,角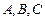 的对边分别是
的对边分别是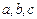 ,满足
,满足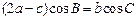 ,求函数
,求函数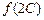 的取值范围
的取值范围
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
(本小题满分15分)
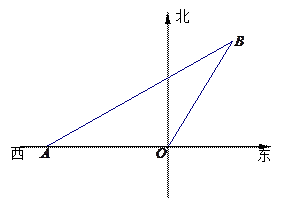
如图,我市现有自市中心 通往正西和东偏北
通往正西和东偏北 方向的两条公路.为了解决市区交通拥挤问题,市政府决定修建一条环城公路,分别在通往正西和东偏北
方向的两条公路.为了解决市区交通拥挤问题,市政府决定修建一条环城公路,分别在通往正西和东偏北 方向的两条公路上选取
方向的两条公路上选取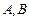 两点,环城公路为
两点,环城公路为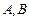 间的直线段,设计要求市中心
间的直线段,设计要求市中心 到
到 段的距离为10km,且
段的距离为10km,且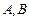 间的距离最小,请你确定
间的距离最小,请你确定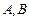 两点的位置
两点的位置
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com