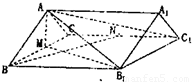
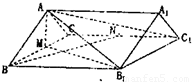
分析:(1)要证A1B⊥CE,应通过证明CE⊥侧面AB1得出.由直棱柱 的性质易证.
(2)取A1B1的中点E1,则C1E1⊥平面ABB1A1,连接E1F,∠C1FE1为C1F与侧面ABB1A1所成角,在直角三角形C1E1F中 求解即可.
(3)容易得知EF∥A1B,∠C1FE是异面直线A1B与C1F所成角(或补角),解三角形C1FE即可.
解答:
解:(1)因为直三棱柱,所以侧面AB
1⊥底面ABC
又因为底面△ABC为等腰直角三角形,E是斜边AB的中点
所以CE⊥AB,所以CE⊥侧面AB
1,而A
1B?侧面AB
1,所以A
1B⊥CE----(4分)
(2)取A
1B
1的中点E
1,则C
1E
1⊥平面ABB
1A
1,连接E
1F
∴∠C
1FE
1为C
1F与侧面ABB
1A
1所成角-------------(6分)
在直角三角形C
1E
1F中,C
1E
1=
A1B1=2,
E1F=2,
∴
tan∠C1FE1==C
1F与侧面ABB
1A
1所成角的正切值为
.-----------(8分)
(3)因为E是AB的中点,F是AA
1的中点,所以EF∥A
1B,
即∠C
1FE是异面直线A
1B与C
1F所成角(或补角)-----(10分)
EF=A1B=,
C1F===C1E===∴C
1E
2=EF
2+C
1F
2,∴∠C
1FE=90°
即异面直线A
1B与C
1F成90
0角.-------(13分)
点评:本题考查直线和直线、直线和平面垂直、平行关系的判定,直线和直线、平面所成角的计算.考查考查空间想象能力、转化、计算、推理论证能力.

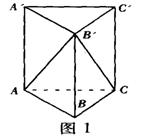
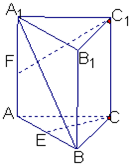 已知直棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,AC=BC=2
已知直棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,AC=BC=2 解:(1)因为直三棱柱,所以侧面AB1⊥底面ABC
解:(1)因为直三棱柱,所以侧面AB1⊥底面ABC

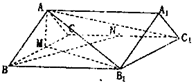 如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点.
如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点.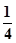 B、
B、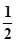 C、
C、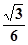 D、
D、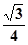
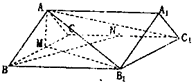 如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点.
如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点.