练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若-
    2π
    3
    ≤θ≤
    2π
    3
    ，则sinθ的取值范围是
     
    ．
    分析：先根据θ的范围可确定-
    π
    2
    、
    π
    2
    均在此范围内，再结合正弦函数的最值和单调性可直接得到答案．
    解答：解：∵-
    2π
    3
    ≤θ≤
    2π
    3
    ，
    当θ=-
    π
    2
    时，sinθ=-1，当θ=
    π
    2
    时，sinθ=1
    ∴-1≤sinθ≤1
    故答案为：[-1，1]
    点评：本题主要考查正弦函数的最值．考查对基础知识的理解程度．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•黄埔区一模）对于函数y=f（x）与常数a，b，若f（2x）=af（x）+b恒成立，则称（a，b）为函数f（x）的一个“P数对”；若f（2x）≥af（x）+b恒成立，则称（a，b）为函数f（x）的一个“类P数对”．设函数f（x）的定义域为R+，且f（1）=3．
    （1）若（1，1）是f（x）的一个“P数对”，求f（2n）（n∈N*）；
    （2）若（-2，0）是f（x）的一个“P数对”，且当x∈[1，2）时f（x）=k-|2x-3|，求f（x）在区间[1，2n）（n∈N*）上的最大值与最小值；
    （3）若f（x）是增函数，且（2，-2）是f（x）的一个“类P数对”，试比较下列各组中两个式子的大小，并说明理由．
    ①f（2-n）与2-n+2（n∈N*）；
    ②f（x）与2x+2（x∈（0，1]）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•枣庄二模）已知抛物线x2=2py上点（2，2）处的切线经过椭圆E：
    y2
    a2
    +
    x2
    b2
    =1(a＞b＞0)    的两个顶点．
    （1）求椭圆E的方程；
    （2）过椭圆E的上顶点A的两条斜率之积为-4的直线与该椭圆交于B，C两点，是否存在一点D，使得直线BC恒过该点？若存在，请求出定点D的坐标；若不存在，请说明理由；
    （3）在（2）的条件下，若△ABC的重心为G，当边BC的端点在椭圆E上运动时，求|GA|2+|GB|2+|GC|2的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2010•上海模拟）以下有四个命题：
    ①一个等差数列{an}中，若存在ak+1＞ak＞O（k∈N），则对于任意自然数n＞k，都有an＞0；
    ②一个等比数列{an}中，若存在ak＜0，ak+1＜O（k∈N），则对于任意n∈N，都有an＜0；
    ③一个等差数列{an}中，若存在ak＜0，ak+1＜0（k∈N），则对于任意n∈N，都有an＜O；
    ④一个等比数列{an}中，若存在自然数k，使ak•ak+1＜0，则对于任意n∈N，都有an．an+1＜0；
    其中正确命题的个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2014届广东省东莞市高二下学期期末考试理科数学试卷（A）（解析版） 题型：解答题

    根据以往资料统计，大学生购买某品牌平板电脑时计划采用分期付款的期数ζ的分布列为

    ζ

    1

    2

    3

    P

    0.4

    0.25

    0.35

    (1)若事件A=｛购买该平板电脑的3位大学生中，至少有1位采用1期付款｝，求事件A的概率P（A）；

    (2)若签订协议后，在实际付款中，采用1期付款的没有变化，采用2、3期付款的都至多有一次改付款期数的机会，其中采用2期付款的只能改为3期，概率为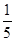；采用3期付款的只能改为2期，概率为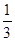.数码城销售一台该平板电脑，实际付款期数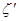与利润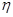（元）的关系为

    1

    2

    3

    η

    200

    250

    300

    (3)求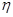的分布列及期望E（）.

     

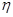    查看答案和解析>>

    同步练习册答案