
圆台的上、下底面半径分别是10 cm和20 cm,它的侧面展开图的扇环的圆心角是180°,那么圆台的表面积是多少?
如图所示,设圆台的上底面周长为c,因为扇环的圆心角是180°,?
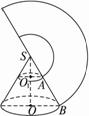
故c=π·SA=2π×10,?
所以SA=20.?
同理可得SB=40,?
所以AB=SB-SA=20.?
所以S表面积=S侧+S上+S下
=π (r1+r2)·AB+πr12+πr22?
=π (10+20)×20+π×102+π×202?
=1 100π (cm)2.?
故圆台的表面积为1 100πcm2.
解答本题可把空间问题转化为平面问题,即先在展开图内求母线的长,再进一步代入侧面积公式求出侧面积,进而求出表面积.
①求圆台的表面积应考虑上、下底面及侧面积;?
②上、下底面面积易得,主要求侧面积.?


科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com