
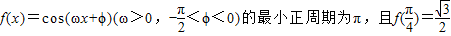 .
.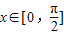 ,求f(x)的取值范围.
,求f(x)的取值范围. ,结合φ的范围即可求得φ的值;(2)将内层函数看做整体,求内层函数的值域,再利用余弦函数的图象和性质求函数的值域;(3)利用余弦曲线的对称中心为(kπ+
,结合φ的范围即可求得φ的值;(2)将内层函数看做整体,求内层函数的值域,再利用余弦函数的图象和性质求函数的值域;(3)利用余弦曲线的对称中心为(kπ+ ,0),解方程即可得此函数的对称中心
,0),解方程即可得此函数的对称中心 的最小正周期为π
的最小正周期为π =π,ω=2
=π,ω=2 ,∴
,∴
 ,又-
,又- <φ<0
<φ<0

 ,∴2x-
,∴2x- ∈[-
∈[- ,
, ]
] ≤f(x)≤1
≤f(x)≤1 =kπ+
=kπ+ ,k∈Z
,k∈Z kπ+
kπ+ ,k∈Z
,k∈Z kπ+
kπ+ ,0)
,0)

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源:2011年江西省八所重点中学高三联考数学试卷(理科)(解析版) 题型:解答题
 其中
其中 .
.
查看答案和解析>>
科目:高中数学 来源:2014届广东雷州一中.徐闻中学高一下学期第二次联考数学卷(解析版) 题型:解答题
(本题满分14分)设函数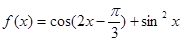 ,
,
(1)求函数 的最大值和最小正周期;
的最大值和最小正周期;
(2)设 为
为 的三个内角,若
的三个内角,若 ,且
,且 为锐角,求
为锐角,求 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:黑龙江省2009-2010学年度上学期高三期末(数学理)试题 题型:解答题
已知集合 ,
, ,且
,且 ,设函数
,设函数 .
.
(1)求函数 的单调减区间;
的单调减区间;
(2)当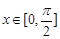 时,求
时,求 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com