
 其中
其中 .
.
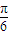 的范围,再由正弦函数的性质以及最小值求出a的值;
的范围,再由正弦函数的性质以及最小值求出a的值;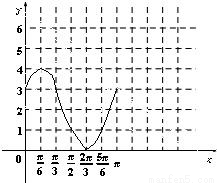 解:(1)由题意知,
解:(1)由题意知,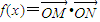
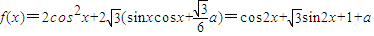

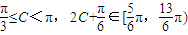 ,
,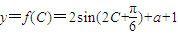 的最小值为2×(-1)+a+1=0,
的最小值为2×(-1)+a+1=0,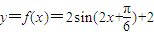 ,
,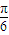 )=4,f(
)=4,f(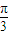 )=3,f(
)=3,f(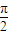 )=1,f(
)=1,f(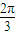 )=0,f(
)=0,f(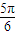 )=1,f(π)=3.
)=1,f(π)=3.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
| OA |
| OB |
| 3 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| OC |
| AP |
| PB |
| CA |
| π |
| 8 |
| π |
| 2 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OPk |
| OB |
| OA |
查看答案和解析>>
科目:高中数学 来源:2012年四川省高考数学压轴卷(理科)(解析版) 题型:解答题
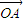 =(sinα,1),
=(sinα,1),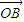 =(cosα,0),
=(cosα,0),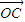 =(-sinα,2),点P是直线AB上的一点,且点B分有向线段
=(-sinα,2),点P是直线AB上的一点,且点B分有向线段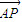 的比为1.
的比为1.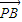 •
•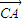 ,α∈(-
,α∈(-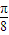 ,
,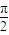 ),讨论函数f(α)的单调性,并求其值域;
),讨论函数f(α)的单调性,并求其值域;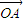 +
+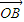 |的值.
|的值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三11月月考文科数学 题型:解答题
(本小题满分12分) (Ⅰ)小问7分,(Ⅱ)小问5分.)
已知O为坐标原点,向量=(sinα,1),=(cosα,0),=(-sinα,2),点P是直线AB上的一点,且点B分有向线段的比为1.
(1)记函数f(α)=·,α∈,讨论函数f(α)的单调性,并求其值域;
(2)若O、P、C三点共线,求|+|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com