练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    (本题满分12分)对甲、乙的学习成绩进行抽样分析，各抽5门功课，得到的观测值如下：
    甲：60　80　70　90　70
    乙：80　60　70　80　75
    问：甲、乙谁的平均成绩好？谁的各门功课较平衡？
    甲的平均成绩较好，乙的各门功课较平衡．
    第一问中，利用给出的数据，结合平均值的公式可知甲，乙，s甲，s乙
    然后根据平均值来看谁的平均数大就是成绩好，而方差越小说明越平稳。
    解：　甲＝×(60＋80＋70＋90＋70)＝74，
    乙＝×(80＋60＋70＋80＋75)＝73，
    s甲＝≈10.2，
    s乙＝≈7.5.
    因为甲>乙，s甲>s乙．
    所以甲的平均成绩较好，乙的各门功课较平衡．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    某中学研究性学习小组，为了考察高中学生的作文水平与爱看课外书的关系，在本校高三年级随机调查了 50名学生.调査结果表明：在爱看课外书的25人中有18人作文水平好，另7人作文水平一般；在不爱看课外书的25人中有6人作文水平好，另19人作文水平一般.
    （Ⅰ）试根据以上数据完成以下2×2列联表，并运用独立性检验思想，指出有多大把握认为中学生的作文水平与爱看课外书有关系？
    高中学生的作文水平与爱看课外书的2×2列联表
     
    		爱看课外书
    		不爱看课外书
    		总计
    作文水平好
    		 
    		 
    		 
    作文水平一般
    		 
    		 
    		 
    总计
    		 
    		 
    		 
    （Ⅱ）将其中某5名爱看课外书且作文水平好的学生分别编号为1、2、3、4、5，某5名爱看课外书且作文水平一般的学生也分别编号为1、2、3、4、5，从这两组学生中各任选1人进行学习交流，求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
    参考公式：，其中.
    参考数据：

    		0.10
    		0.05
    		0.025
    		0.010
    		0.005
    		0.001

    		2.706
    		3.841
    		5.024
    		6.635
    		7.879
    		10.828

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （10分）某种产品的广告费支出x与消费额y(单位：百万元)之间有如下对应数据：
    x
    		2
    		4
    		5
    		6
    		8
    y
    		30
    		40
    		60
    		50
    		70
    (1)求线性回归方程；
    (2)预测当广告费支出为700万元时的销售额．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

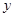    在两个变量与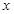的回归模型中,分别选择了4个不同的模型,它们的相关指数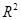分别为:模型1的相关指数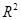为0.98,模型2的相关指数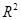为0.80,模型3的相关指数为0.50,模型4的相关指数为0.25.其中拟合效果最好的是(     )
    A．模型1B．模型2C．模型3D．模型4

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

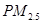    是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，上图是据北京某日早7点至晚8点甲、乙两个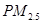监测点统计的数据（单位：毫克/每立方米）列出的茎叶图，则甲、乙两地浓度的中位数较低的是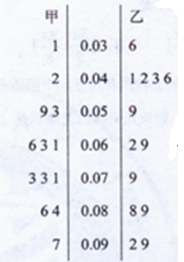
    A．甲乙相等B．甲C．乙D．无法确定

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    从学号为0～50的高一某班50名学生中随机选取5名同学参加数学测试,采用系
    统抽样的方法,则所选5名学生的学号可能是：（  ）
    A．5,15,25,35,45B．1,2,3,4,5
    C．2,4,6,8,10D．4,13,22,31,40

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

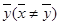    样本（x1,x2…，xn）的平均数为x，样本（y1，y2，…，yn）的平均数为。若样本（x1,x2…，xn，y1，y2，…，yn）的平均数，其中0＜α＜，则n，m的大小关系为
    A．n＜mB．n＞mC．n=mD．不能确定

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    、一位母亲记录了儿子3～9岁的身高，由此建立的身高与年龄的回归模型为
    y=7.19x+73.93用这个模型预测这个孩子10岁时的身高，则正确的叙述是（   ）
    A．身高一定是145.83cmB．身高在145.83cm以上
    C．身高在145.83cm以下D．身高在145.83cm左右

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    甲、乙、丙、丁四位同学去书店购买编号为１，２，３，４，…，１０的１０本不同的书，为节约起见，他们约定每人只购买其中５本，再互相传阅，如果任两人均不能买全这１０本书，任３人均能买全这１０本书，其中甲购买数的号码是１，２，３，４，５，乙购买书的号码事５，６，７，８，９，丙购买书的号码是１，２，３，９，１０时，为了满足上述要求，丁应买的书的号码是　　     　；

    查看答案和解析>>

    同步练习册答案