
【题目】“中国人均读书4.3本(包括网络文学和教科书),比韩国的11本、法国的20本、日本的40本、犹太人的64本少得多,是世界上人均读书最少的国家.”这个论断被各种媒体反复引用.出现这样的统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天![]() 名读书者进行调查,将他们的年龄分成6段:
名读书者进行调查,将他们的年龄分成6段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
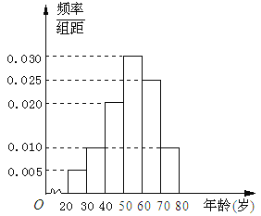
,![]() 后得到如图所示的频率分布直方图.问:
后得到如图所示的频率分布直方图.问:
(1)估计在40名读书者中年龄分布在![]() 的人数;
的人数;
(2)求40名读书者年龄的平均数和中位数;
(3)若从年龄在![]() 的读书者中任取2名,求这两名读书者年龄在
的读书者中任取2名,求这两名读书者年龄在![]() 的人数
的人数![]() 的分布列及数学期望.
的分布列及数学期望.
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() ,曲线
,曲线![]() :
: ![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线![]() ,
, ![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ,
, ![]() )分别交
)分别交![]() ,
, ![]() 于
于![]() ,
, ![]() 两点,当
两点,当![]() 取何值时,
取何值时, ![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足an=2Sn﹣1(n∈N*) (Ⅰ)求证:数列{an}为等比数列;
(Ⅱ)若bn=(2n+1)an , 求{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
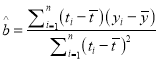 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)估计用电量落在[220,300)中的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(第x周)和市场占有率(y﹪)的几组相关数据如下表:
| 1 | 2 | 3 | 4 | 5 |
| 0.03 | 0.06 | 0.1 | 0.14 | 0.17 |
(Ⅰ)根据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)根据上述线性回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测在第几周,该款旗舰机型市场占有率将首次超过 0.40﹪(最后结果精确到整数).
参考公式: ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com