下列四个命题中的假命题是( )
A.存在这样的α、β,使得cos(α+β)=cosαcosβ-sinαsinβ
B.不存在无穷多个α、β,使得cos(α+β)=cosαcosβ-sinαsinβ
C.对于任意的α、β,cos(α+β)=cosαcosβ-sinαsinβ
D.不存在这样的α、β,使得cos(α+β)≠cosαcosβ-sinαsinβ
【答案】分析:对A,由两角和的余弦定理可知存在这样的α、β,使得cos(α+β)=cosαcosβ+sinαsinβ,即可判断;
对B,由cos(α+β)=cosαcosβ+sinαsinβ=cosαcosβ-sinαsinβ,得sinαsinβ=0.∴α=kπ或β=kπ(k∈Z),即可判断;
对C,对于任意的α、β,cos(α+β)=cosαcosβ-sinαsinβ,即可得出答案;
对D,不存在这样的α、β,使得cos(α+β)≠cosαcosβ-sinαsinβ,即可判断真假;
解答:解:对A,由两角和的余弦定理可知存在这样的α、β,使得cos(α+β)=cosαcosβ+sinαsinβ,故本选项为真命题;
对B,由cos(α+β)=cosαcosβ+sinαsinβ=cosαcosβ-sinαsinβ,得sinαsinβ=0.∴α=kπ或β=kπ(k∈Z),故本选项为假命题.
对C,对于任意的α、β,由两角和的余弦公式可得:cos(α+β)=cosαcosβ-sinαsinβ,故本选项为真命题;
对D,不存在这样的α、β,使得cos(α+β)≠cosαcosβ-sinαsinβ,若存在α,β,则与两角和的余弦公式矛盾,故本选项为真命题;
故选B.
点评:本题考查了四种命题的真假关系及两角和与差的余弦函数,属于基础题,关键是掌握两角和的余弦函数公式.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,有下列四个命
,有下列四个命 ; B.在所有
; B.在所有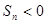 中,
中, 最大;
最大;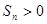 的
的 的个数有11个; D.
的个数有11个; D. ;
;