
【题目】已知数列{an}中,a2=2,前n项和为 ![]() . (I)证明数列{an+1﹣an}是等差数列,并求出数列{an}的通项公式;
. (I)证明数列{an+1﹣an}是等差数列,并求出数列{an}的通项公式;
(II)设 ![]() ,数列{bn}的前n项和为Tn , 求使不等式
,数列{bn}的前n项和为Tn , 求使不等式 ![]() 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
【答案】解:(I)由题意,当 ![]() . a2=2,则a2﹣a1=1.
. a2=2,则a2﹣a1=1.
当 ![]() ,
, ![]() ,
,
则 ![]() ,
,
则(n﹣1)an+1﹣2(n﹣1)an+(n﹣1)an﹣1=0,
即an+1﹣2an+an﹣1=0,
即an+1﹣an=an﹣an﹣1 .
则数列{an+1﹣an}是首项为1,公差为0的等差数列.
从而an﹣an﹣1=1,则数列{an}是首项为1,公差为1的等差数列.
所以,an=n(n∈N*)
(II) ![]()
所以, 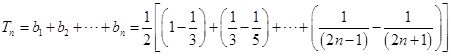
= ![]() .
.
由于 ![]() .
.
因此Tn单调递增,
故Tn的最小值为 ![]()
令 ![]() ,
,
所以k的最大值为18
【解析】(I)由题意,当 ![]() .a2=2,则a2﹣a1=1.当
.a2=2,则a2﹣a1=1.当 ![]() ,由此入手能够导出数列{an+1﹣an}是首项为1,公差为0的等差数列,从而能够求出an . (II)
,由此入手能够导出数列{an+1﹣an}是首项为1,公差为0的等差数列,从而能够求出an . (II) ![]() ,所以,
,所以, ![]() =
= ![]() .由此能够求出使不等式
.由此能够求出使不等式 ![]() 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
【考点精析】关于本题考查的等差数列的通项公式(及其变式)和等差关系的确定,需要了解通项公式:![]() 或
或![]() ;如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即
;如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列才能得出正确答案.
)那么这个数列就叫做等差数列才能得出正确答案.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( ) 
A.2,5
B.2,4
C.0,4
D.0,5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() =1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为
=1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为 ![]() .
. 
(1)求椭圆方程;
(2)若 ![]() ,求直线PQ的方程;
,求直线PQ的方程;
(3)M,N为椭圆上关于x轴对称的两点,直线PM,PN分别与x轴交于R,S,求证:|OR||OS|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=5,a2=2,an=2an﹣1+3an﹣2 , (n≥3) (Ⅰ)证明数列{an﹣3an﹣1}成等比数列,并求数{an}列的通项公式an;
(Ⅱ)若数列bn= ![]() (an+1+an),求数列{bn}的前n项和Sn .
(an+1+an),求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一艘海轮从A出发,沿北偏东75°的方向航行(2 ![]() ﹣2)nmile到达海岛B,然后从B出发,沿北偏东15°的方向航行4nmile到达海岛C.
﹣2)nmile到达海岛B,然后从B出发,沿北偏东15°的方向航行4nmile到达海岛C. 
(1)求AC的长;
(2)如果下次航行直接从A出发到达C,求∠CAB的大小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(ωx+φ)(A,ω>0,0<|φ|<π)在一个周期内的图象如图所示.
(1)求函数f(x)的解析式;
(2)求g(x)=f(3x+![]() )﹣1在[﹣
)﹣1在[﹣![]() ,
, ![]() ]上的值域.
]上的值域.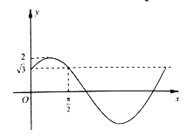
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥S﹣ABCD中,侧棱与底面所成的角为α,侧面与底面所成的角为β,侧面等腰三角形的底角为γ,相邻两侧面所成的二面角为θ,则α、β、γ、θ的大小关系是( )
A.α<β<γ<θ
B.α<β<θ<γ
C.θ<α<γ<β
D.α<γ<β<θ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
(Ⅰ)求证:平面EAC⊥平面PBC;
(Ⅱ)若二面角P﹣AC﹣E的余弦值为 ![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com