
若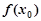 是函数
是函数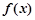 在点
在点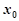 附近的某个局部范围内的最大(小)值,则称
附近的某个局部范围内的最大(小)值,则称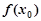 是函数
是函数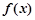 的一个极值,
的一个极值,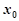 为极值点.已知
为极值点.已知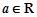 ,函数
,函数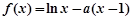 .
.
(Ⅰ)若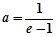 ,求函数
,求函数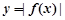 的极值点;
的极值点;
(Ⅱ)若不等式 恒成立,求
恒成立,求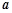 的取值范围.
的取值范围.
(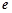 为自然对数的底数)
为自然对数的底数)
(1) 的极小值点为1和
的极小值点为1和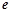 ,极大值点为
,极大值点为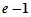 .
.
(2)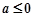
【解析】
试题分析:解:(Ⅰ)若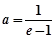 ,则
,则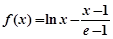 ,
,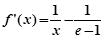 .
.
当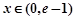 时,
时,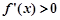 ,
,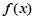 单调递增;
单调递增;
当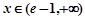 时,
时,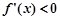 ,
,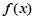 单调递减. …2分
单调递减. …2分
又因为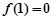 ,
,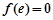 ,所以
,所以
当 时,
时,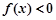 ;当
;当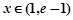 时,
时, ;
;
当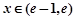 时,
时, ;当
;当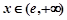 时,
时,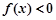 . …4分
. …4分
故 的极小值点为1和
的极小值点为1和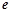 ,极大值点为
,极大值点为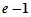 . …6分
. …6分
(Ⅱ)不等式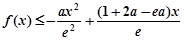 ,
,
整理为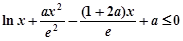 .…(*)
.…(*)
设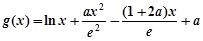 ,
,
则 (
(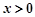 )
)
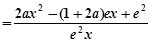
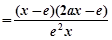 . …8分
. …8分
①当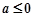 时,
时,
 ,又
,又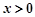 ,所以,
,所以,
当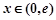 时,
时,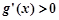 ,
,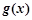 递增;
递增;
当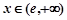 时,
时,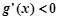 ,
,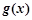 递减.
递减.
从而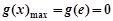 .
.
故,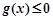 恒成立. …11分
恒成立. …11分
②当 时,
时,
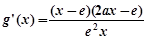
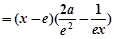 .
.
令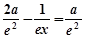 ,解得
,解得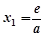 ,则当
,则当 时,
时,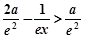 ;
;
再令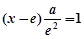 ,解得
,解得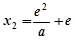 ,则当
,则当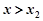 时,
时,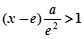 .
.
取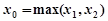 ,则当
,则当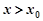 时,
时, .
.
所以,当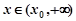 时,
时,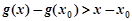 ,即
,即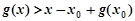 .
.
这与“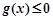 恒成立”矛盾.
恒成立”矛盾.
综上所述,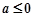 . …14分
. …14分
考点:导数的运用
点评:解决的关键是对于导数在研究函数中的运用,求解极值和最值,以及不等式的恒成立问题,属于基础题。


科目:高中数学 来源: 题型:
(07年湖南卷文)(13分)
已知函数![]() 在区间
在区间![]() 内各有一个极值点.
内各有一个极值点.
(Ⅰ)求![]() 的最大值;
的最大值;
(Ⅱ)当![]() 时,设函数
时,设函数![]() 在点
在点![]() 处的切线为
处的切线为![]() ,若在点A处穿过
,若在点A处穿过![]() 的图象(即动点在点A附近沿曲线
的图象(即动点在点A附近沿曲线![]() 运动,经过点A时,从
运动,经过点A时,从![]() 的一侧进入另一侧),求函数
的一侧进入另一侧),求函数![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
函数![]() ,其中
,其中![]() 、
、![]()
![]() 是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数
是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数![]() ,在点
,在点![]() 附近一点
附近一点![]() 的函数值
的函数值![]() ,可以用如下方法求其近似代替值:
,可以用如下方法求其近似代替值:![]() .利用这一方法,
.利用这一方法,![]() 的近似代替值
的近似代替值
A.大于![]() B.小于
B.小于![]() C.等于
C.等于![]() D.与
D.与![]() 的大小关系无法确定
的大小关系无法确定
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试文科数学卷(湖南) 题型:解答题
(本小题满分13分)
已知函数 在区间
在区间 ,
, 内各有一个极值点.
内各有一个极值点.
(I)求 的最大值;
的最大值;
(II)当 时,设函数
时,设函数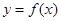 在点
在点 处的切线为
处的切线为 ,若
,若 在点
在点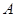 处穿过函数
处穿过函数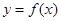 的图象(即动点在点
的图象(即动点在点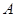 附近沿曲线
附近沿曲线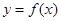 运动,经过点
运动,经过点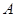 时,从
时,从 的一侧进入另一侧),求函数
的一侧进入另一侧),求函数 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() 在区间
在区间![]() 内各有一个极值点.
内各有一个极值点.
(Ⅰ)求![]() 的最大值;
的最大值;
(Ⅱ)当![]() 时,设函数
时,设函数![]() 在点
在点![]() 处的切线为
处的切线为![]() ,若
,若![]() 在点A处穿过
在点A处穿过![]() 的图象(即动点在点A附近沿曲线
的图象(即动点在点A附近沿曲线![]() 运动,经过点A时,从
运动,经过点A时,从![]() 的一侧进入另一侧),求函数
的一侧进入另一侧),求函数![]() 的表达式.
的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com