Question

已知直线l₁过点A（-2，3），B（4，m），直线l₂过点M（1，0），N（0，m-4），若l₁⊥l₂，则常数m的值是    ．

Answer 1

【答案】分析：由斜率公式分别可得两直线的斜率，由垂直关系易得其乘积为-1，解之可得m的值．
解答：解：∵直线l₁过点A（-2，3），B（4，m），
∴直线l₁的斜率k₁==，
同理直线l₂过点M（1，0），N（0，m-4），
故直线l₂的斜率k₂=，
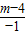
因为l₁⊥l₂，所以k₁•k₂==-1，
即m²-7m+6=0，分解因式可得（m-1）（m-6）=0，
解得m=1或m=6，
故答案为：1或6
点评：本题考查直线的垂直关系，以及直线的斜率公式的运用，属基础题．