
(1)若 在
在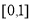 上单调递减,求
上单调递减,求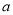 的取值范围.
的取值范围.
(2)若使函数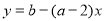 和
和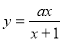 都在
都在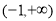 上单调递增,求
上单调递增,求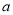 的取值范围.
的取值范围.
(1) ;(2)
;(2)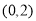 .
.
【解析】
试题分析:(1)根据题意知,函数 的定义域满足:
的定义域满足: 在
在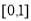 上恒成立,且函数
上恒成立,且函数 在
在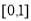 上单调递减,分别运用变量分离法和二次函数的单调性求出参数
上单调递减,分别运用变量分离法和二次函数的单调性求出参数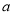 所满足的取值范围,取交集即可得出答案;(2)分别根据一次函数的图像和反比例函数图像知,当
所满足的取值范围,取交集即可得出答案;(2)分别根据一次函数的图像和反比例函数图像知,当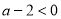 时,函数
时,函数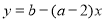 为单调递增的; 当
为单调递增的; 当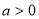 时,
时, 在
在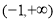 上单调递增.
上单调递增.
试题解析:(1)由题意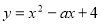 在
在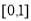 上单调递减且
上单调递减且 在
在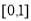 上恒成立.
上恒成立.
若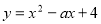 在
在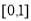 上单调递减,则
上单调递减,则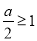 ,即
,即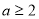 ;由
;由 在
在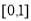 上恒成立得
上恒成立得 ,当
,当 时显然成立;
时显然成立;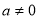 时可得:
时可得: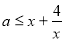 在
在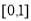 上恒成立.
上恒成立.
因为 ,所以
,所以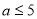 ,故
,故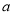 的取值范围是
的取值范围是 .
.
(2)由函数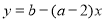 在
在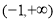 单调递增得:
单调递增得: 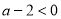 ,所以
,所以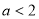 .
.
又因为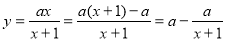 在
在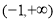 上单调递增,所以
上单调递增,所以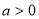 .
.
综上所述: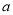 的取值范围是
的取值范围是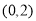 .
.
考点:二次函数的单调性;一次函数的单调性;反比例函数的单调性.


科目:高中数学 来源:2016届辽宁省锦州市高一下学期期末数学试卷(解析版) 题型:选择题
已知实数x,y满足0≤x≤2π,|y|≤1则任意取期中的x,y使y>cosx的概率为( )
A.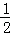 B.
B.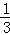 C.
C.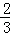 D.无法确定
D.无法确定
查看答案和解析>>
科目:高中数学 来源:2016届辽宁省葫芦岛市高一上学期第一次月考数学试卷(解析版) 题型:填空题
函数设 为实常数,
为实常数,  是定义在R上的奇函数,当
是定义在R上的奇函数,当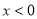 时,
时, 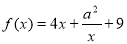 ,若
,若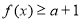 对一切
对一切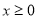 恒成立,则
恒成立,则 的取值范围为 .
的取值范围为 .
查看答案和解析>>
科目:高中数学 来源:2016届辽宁省葫芦岛市高一上学期第一次月考数学试卷(解析版) 题型:选择题
已知函数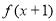 的定义域为
的定义域为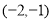 ,则函数
,则函数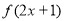 的定义域为( )
的定义域为( )
A.(-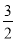 ,-1) B.(-1,-
,-1) B.(-1,-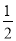 ) C.(-5,-3) D.(-2,-
) C.(-5,-3) D.(-2,-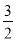 )
)
查看答案和解析>>
科目:高中数学 来源:2016届辽宁省分校高一下学期期末考试数试卷(解析版) 题型:解答题
甲有大小相同的两张卡片,标有数字2、3;乙有大小相同的卡片四张,分别标有1、2、3、4.
(1)求乙随机抽取的两张卡片的数字之和为奇数的概率;
(2)甲、乙分别取出一张卡,比较数字,数字大者获胜,求乙获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com