
 边形
边形 中的每条边和每条对角线都被染为n种颜色中的一种颜色.问:对怎样的n,存在一种染色方式,使得对于这n种颜色中的任何3种不同颜色,都能找到一个三角形,其顶点为多边形
中的每条边和每条对角线都被染为n种颜色中的一种颜色.问:对怎样的n,存在一种染色方式,使得对于这n种颜色中的任何3种不同颜色,都能找到一个三角形,其顶点为多边形 的顶点,且它的3条边分别被染为这3种颜色?
的顶点,且它的3条边分别被染为这3种颜色?
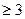 为奇数时,存在合乎要求的染法;当
为奇数时,存在合乎要求的染法;当
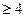 为偶数时,不存在所述的染法。
为偶数时,不存在所述的染法。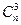 个,而颜色的三三搭配也刚好有
个,而颜色的三三搭配也刚好有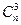 种,所以本题相当于要求不同的三角形对应于不同的颜色组合,即形成一一对应.
种,所以本题相当于要求不同的三角形对应于不同的颜色组合,即形成一一对应.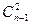 种搭配,所以每种颜色的线段(边或对角线)都应出现在
种搭配,所以每种颜色的线段(边或对角线)都应出现在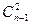 个三角形中,这表明在合乎要求的染法中,各种颜色的线段条数相等.所以每种颜色的线段都应当有
个三角形中,这表明在合乎要求的染法中,各种颜色的线段条数相等.所以每种颜色的线段都应当有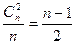 条.
条. 为偶数时,
为偶数时,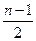 不是整数,所以不可能存在合乎条件的染法.下设
不是整数,所以不可能存在合乎条件的染法.下设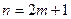 为奇数,我们来给出一种染法,并证明它满足题中条件.自某个顶点开始,按顺时针方向将凸
为奇数,我们来给出一种染法,并证明它满足题中条件.自某个顶点开始,按顺时针方向将凸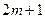 边形的各个顶点依次记为
边形的各个顶点依次记为 .对于
.对于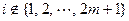 ,按
,按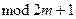 理解顶点
理解顶点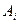 .再将
.再将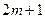 种颜色分别记为颜色
种颜色分别记为颜色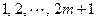 .
.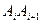 染为颜色
染为颜色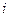 ,其中
,其中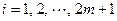 .再对每个
.再对每个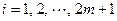 ,都将线段(对角线)
,都将线段(对角线)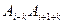 染为颜色
染为颜色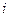 ,其中
,其中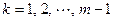 .于是每种颜色的线段都刚好有
.于是每种颜色的线段都刚好有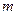 条.注意,在我们的染色方法之下,线段
条.注意,在我们的染色方法之下,线段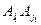 与
与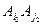 同色,当且仅当
同色,当且仅当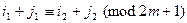 . ①
. ①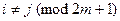 ,任何
,任何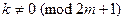 ,线段
,线段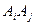 都不与
都不与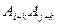 同色.换言之,如果
同色.换言之,如果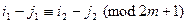 . ②
. ②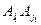 都不与
都不与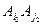 同色.
同色.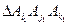 和
和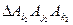 ,如果它们之间至多只有一条边同色,当然它们不对应相同的颜色组合.如果它们之间有两条边分别同色,我们来证明第3条边必不同颜色.为确定起见,不妨设
,如果它们之间至多只有一条边同色,当然它们不对应相同的颜色组合.如果它们之间有两条边分别同色,我们来证明第3条边必不同颜色.为确定起见,不妨设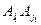 与
与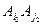 同色.
同色.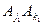 与
与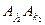 也同色,则由①知
也同色,则由①知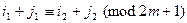 ,
, 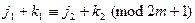 ,
, 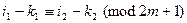 ,故由②知
,故由②知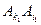 不与
不与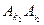 同色.
同色.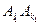 与
与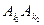 也同色,则亦由①知
也同色,则亦由①知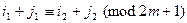 ,
,  ,
, 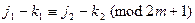 ,亦由②知
,亦由②知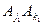 与
与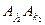 不同色.总之,
不同色.总之,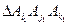 与
与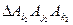 对应不同的颜色组合.
对应不同的颜色组合. 

科目:高中数学 来源:不详 题型:解答题
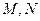 是椭圆
是椭圆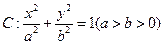 上关于原点
上关于原点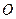 对称的两个点,点
对称的两个点,点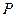 是椭圆
是椭圆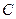 上任意一点,且直线
上任意一点,且直线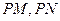 的斜率都存在(记为
的斜率都存在(记为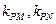 ),则
),则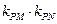 是与点
是与点 位置无关的定值。试写出双曲线
位置无关的定值。试写出双曲线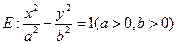 的类似性质,并加以证明。
的类似性质,并加以证明。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (x≠-
(x≠- ,a>0),且f(1)=log162,f(-2)=1.
,a>0),且f(1)=log162,f(-2)=1.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
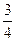 ,sin215°+cos245°+sin15°·cos45°=
,sin215°+cos245°+sin15°·cos45°=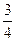 ,
,查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(1)(2) | B.(1)(3)(4) | C.(1)(2)(4) | D.(2)(4) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.正方形都是对角线相等的四边形 | B.矩形都是对角线相等的四边形 |
| C.等腰梯形都是对角线相等的四边形 | D.矩形都是对边相等且平行的四边形 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ”类比推出“若a,b
”类比推出“若a,b ”;
”; ”类比推出“若a,b,c,d
”类比推出“若a,b,c,d
 ”;
”; ” 类比推出“若a,b
” 类比推出“若a,b ”;
”;| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com