
科目:高中数学 来源: 题型:
已知函数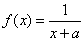 ,
,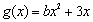 .
.
(Ⅰ)若曲线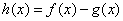 在点(1,0)处的切线斜率为0,求a,b的值;
在点(1,0)处的切线斜率为0,求a,b的值;
(Ⅱ)当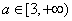 ,且ab=8时,求函数
,且ab=8时,求函数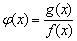 的单调区间,并求函数在区间[-2,-1]上的最小值。
的单调区间,并求函数在区间[-2,-1]上的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知动点P到点A(-2,0)与点B(2,0)的斜率之积为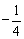 ,点P的轨迹为曲线C。
,点P的轨迹为曲线C。
(Ⅰ)求曲线C的方程;
(Ⅱ)若点Q为曲线C上的一点,直线AQ,BQ与直线x=4分别交于M、N两点,直线BM与椭圆的交点为D。求线段MN长度的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知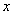 、
、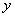 的取值如右表所示:从散点图分析,
的取值如右表所示:从散点图分析,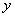 与
与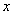 线性相关,且
线性相关,且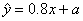 ,则
,则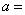 ( )
( )
A. 0.8 B. 1 C. 1.2 D. 1.5
|
| 0 | 1 | 3 | 4 |
|
| 0.9 | 1.9 | 3.2 | 4.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
某学校900名学生在一次百米测试中,成绩全部介于 秒与
秒与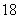 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组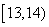 ,第二组
,第二组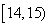 ,…,第五组
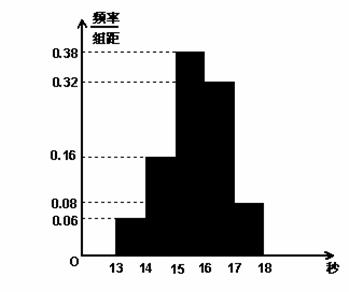
,…,第五组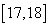 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计学校900名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数和中位数(保留两位小数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com