
已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M

(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程
(1) 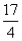
(2)见解析;
【解析】(1)由题意可知,抛物线的准线方程为:y=-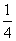 所以圆心M(0,4)到准线的距离是
所以圆心M(0,4)到准线的距离是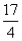
(2) 设P(x0,x02),A(x1,x12),B(x2,x22),
则由题意得x0≠0,x0≠±1,x1≠x2,
设过点P的圆C2的切线方程为y-x02=k(x-x0),
即kx-y-kx0 +x02=0 ①
则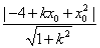 =1
=1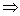 ( x02-1)k2+2 x0(4-x02)k+( x02-4)2-1=0,
( x02-1)k2+2 x0(4-x02)k+( x02-4)2-1=0,
设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2是上述方程的两根,所以
k1+k2= 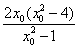 ,k1·k2=
,k1·k2=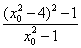
将①代入x2=y得x2 –kx+kx0-x02=0由于x0是此方程的根,点A或B是过点P作圆C2的两条切线与抛物线C1相交的交点
故,x0+x1=k1,x0+x2=k2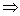 x1=k1-x0,x2=k2- x0
x1=k1-x0,x2=k2- x0
所以kAB= 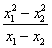 = x1+x2= k1+k2-2x0=
= x1+x2= k1+k2-2x0=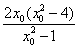 -2x0
-2x0
又KMP=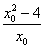
∵MP⊥AB
∴kAB·KMP=[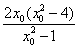 -2x0]·(
-2x0]·(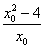 )=-1,
)=-1,
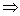
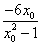 ·
·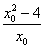 =-1,解
=-1,解 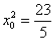
∴即点P的坐标为(±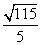 ,
,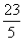 ),KMP=
),KMP=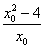 =
=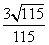
所以直线l的方程为y=±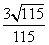 x+4
x+4


科目:高中数学 来源:2014高考名师推荐数学理科正弦定理(解析版) 题型:选择题
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10 m到位置D,测得∠BDC=45°,则塔AB的高是( )

A.10m
B.10 m
m
C.10 m
m
D.10 m
m
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科数列的概念、等差数列、等比数列(解析版) 题型:选择题
已知等比数列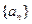 的公比为q,记
的公比为q,记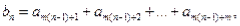
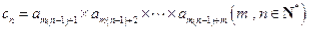 ,则以下结论一定正确的是( )
,则以下结论一定正确的是( )
A.数列 为等差数列,公差为
为等差数列,公差为 B.数列
B.数列 为等比数列,公比为
为等比数列,公比为
C.数列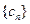 为等比数列,公比为
为等比数列,公比为 D.数列
D.数列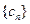 为等比数列,公比为
为等比数列,公比为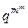
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科排列组合综合应用(解析版) 题型:选择题
现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张.从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张.不同取法的种数为( )
A.232
B.252
C.472
D.484
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科抛物线(解析版) 题型:选择题
已知抛物线关于 轴对称,它的顶点在坐标原点
轴对称,它的顶点在坐标原点 ,并且经过点
,并且经过点 。若点
。若点 到该抛物线焦点的距离为
到该抛物线焦点的距离为 ,则
,则 ( )
( )
A.
B.
C.4
D.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科对数与对数函数(解析版) 题型:填空题
定义“正对数”: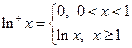 现有四个命题:
现有四个命题:
①若 ,则
,则 ;
;
②若 ,则
,则 ;
;
③若 ,则
,则 ;
;
④若 ,则
,则 .
.
其中的真命题有 .(写出所有真命题的编号)
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科双曲线(解析版) 题型:填空题
已知双曲线 的左,右焦点分别为
的左,右焦点分别为 ,点P在双曲线的右支上,且
,点P在双曲线的右支上,且 ,则此双曲线的离心率e的取值范围是________.
,则此双曲线的离心率e的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com