
(10分) 如图所示,已知 、
、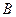 两点的距离为
两点的距离为 海里,
海里,
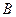 在
在 的北偏东
的北偏东 处,甲船自
处,甲船自 以
以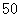 海里/小时的速度向
海里/小时的速度向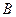 航行,同时乙船自
航行,同时乙船自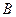 以
以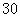 海里/小时的速度沿方位角
海里/小时的速度沿方位角 方向航行。问航行几小时两船之
方向航行。问航行几小时两船之 间的距离最短?
间的距离最短?
科目:高中数学 来源: 题型:解答题
三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.)
16. (本小题满分12分)
已知向量 ,定义函数
,定义函数
(Ⅰ)求函数 最小正周期;
最小正周期;
(Ⅱ)在△ABC中,角A为锐角,且 ,求边AC的长.
,求边AC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数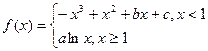
 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点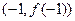 处的切线的斜率是
处的切线的斜率是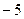 .
.
(Ⅰ)求实数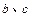 的值;
的值;
(Ⅱ)求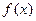 在区间
在区间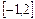 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数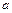 ,曲线
,曲线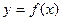 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得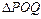 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在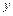 轴上?说明理由。
轴上?说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
港口 北偏东
北偏东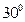 方向的
方向的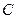 处有一检查站,港口正东方向的
处有一检查站,港口正东方向的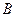 处有一轮船,距离检查站为31海里,该轮船从
处有一轮船,距离检查站为31海里,该轮船从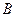 处沿正西方向航行20海里后到达
处沿正西方向航行20海里后到达 处观测站,已知观测站与检查站距离21海里,问此时轮船离港口
处观测站,已知观测站与检查站距离21海里,问此时轮船离港口 还有多远?
还有多远?
|
|
|
|

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com