解:(1)a
n+1=2a
n-n+1,∴a
n+1-(n+1)=2(a
n-n),∴

,
又a
1-1=-2,∴数列{a
n-n}是以2为公比、以-2为首项的等比数列,
∴a
n-n=(-2)•2
n-1=-2
n,∴a
n=n-2
n(2)由(1)得:

,∴


,∴

,
令

,则

,
两式相减得:

∴

,即

,∴
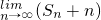
=2.
(3)∵

令

,则

,
当x≥1时,

,
∴f(x)在[1,+∞)单调递减,∴S
n+n-2b
n单调递增,∴

,
∴

,∴若总存在正自然数n,使S
n+n-2b
n<m成立,则
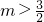
.
分析:(1)将题设中的条件a
n+1=2a
n-n+1变形为a
n+1-(n+1)=2(a
n-n),从而可得数列{a
n-n}是等比数列,进而可得数列{a
n}的通项公式;
(2)由(1)结论可求出b
n,由通项公式的形式可以看出,本题宜先用分组求和的技巧,然后对其一部分用错位减法求和.最后再求极限.
(3)构建函数

,用导数的方法可知f(x)在[1,+∞)单调递减,从而S
n+n-2b
n单调递增.要使总存在正自然数n,S
n+n-2b
n<m成立,只需求 S
n+n-2b
n的最大值,从而得解.
点评:本题意数列递推式为载体,考查数列的通项及求和,是一道综合性较强的题,要观察分析,判断,选择合适的方法,如(1)的求解要从证明的结论中找变形方向;(2)中的求解要边变形边观察,化整为零,分块求解,这对答题者分析判断的能力要求较高;(3)则利用函数的思想,研究其单调性

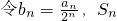 为数列{bn}的前n项和,求
为数列{bn}的前n项和,求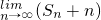 ;
; ,
, ,∴
,∴
 ,∴
,∴ ,
, ,则
,则 ,
,
 ,即
,即 ,∴
,∴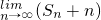 =2.
=2.
 ,则
,则 ,
, ,
, ,
, ,∴若总存在正自然数n,使Sn+n-2bn<m成立,则
,∴若总存在正自然数n,使Sn+n-2bn<m成立,则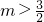 .
. ,用导数的方法可知f(x)在[1,+∞)单调递减,从而Sn+n-2bn单调递增.要使总存在正自然数n,Sn+n-2bn<m成立,只需求 Sn+n-2bn的最大值,从而得解.
,用导数的方法可知f(x)在[1,+∞)单调递减,从而Sn+n-2bn单调递增.要使总存在正自然数n,Sn+n-2bn<m成立,只需求 Sn+n-2bn的最大值,从而得解.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案