
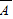 为“5位同学的贺年卡末位数字均不相同”,由分步计数原理可得5位同学,每人买一张有奖贺年卡,5人的末位数字的情况数目,以及5人的末尾数字均不相同的情况数目,由等可能事件的概率公式可得P(
为“5位同学的贺年卡末位数字均不相同”,由分步计数原理可得5位同学,每人买一张有奖贺年卡,5人的末位数字的情况数目,以及5人的末尾数字均不相同的情况数目,由等可能事件的概率公式可得P(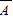 ),利用对立事件的概率性质可得P(A),即可得答案.
),利用对立事件的概率性质可得P(A),即可得答案.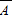 为“5位同学的贺年卡末位数字均不相同”,
为“5位同学的贺年卡末位数字均不相同”,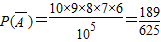 ;
;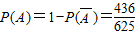 .
.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com