
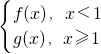 .P(x1,F(x1)),Q(x2,F(x2))为曲线y=F(x)上的两动点,O为坐标原点,能否使得△POQ是以O为直角顶点的直角三角形,且斜边中点在y轴上?请说明理由.
.P(x1,F(x1)),Q(x2,F(x2))为曲线y=F(x)上的两动点,O为坐标原点,能否使得△POQ是以O为直角顶点的直角三角形,且斜边中点在y轴上?请说明理由. ,∴函数g(x)的单调递减区间为(0,
,∴函数g(x)的单调递减区间为(0, ),
), ,∴函数g(x)的单调递增区间为(
,∴函数g(x)的单调递增区间为( ,+∞);
,+∞); ;
;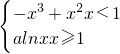 ,
, ,且x1+x2=0,不妨设x1=t>0,
,且x1+x2=0,不妨设x1=t>0, =-t2+F(t)(t3+t2)=0(*)该方程有解,
=-t2+F(t)(t3+t2)=0(*)该方程有解, =(1,0),
=(1,0),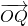 =(-1,2),
=(-1,2), ≠0;
≠0; =(t+1)lnt,
=(t+1)lnt, +1>0在[1,+∞)恒成立,
+1>0在[1,+∞)恒成立, =(t+1)lnt有解,即方程(*)有解,
=(t+1)lnt有解,即方程(*)有解, ,且x1+x2=0,不妨设x1=t>0,可得PQ的坐标,进而可得数量积,分0<t<1,t=1,和t>1讨论可得结论.
,且x1+x2=0,不妨设x1=t>0,可得PQ的坐标,进而可得数量积,分0<t<1,t=1,和t>1讨论可得结论.

科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com