与圆C:x2+y2-2x-2y+1=0相切的直线与x轴,y轴的正半轴交于A、B且|oA|>2,|OB|>2,则三角形AOB面积的最小值为 ________.
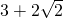
分析:把圆的方程化为标准式方程后,找出圆心坐标和半径,设出A和B的坐标,利用A和B的坐标写出直线AB的方程,因为直线AB与圆相切,利用点到直线的距离公式表示出圆心到直线的距离d,并让d等于半径r,列出关于a和b的关系式,然后设a-2等于m大于0,b-2等于n大于0,利用三角形的面积公式表示出三角形AOB的面积,利用基本不等式求出面积的最小值即可.
解答:将圆C的方程化为标准式方程得(x-1)
2+(y-1)
2=1,圆心C(1,1),半径r=1
设A(a,0),B(0,b),则直线AB的方程为

+

=1,即bx+ay-ab=0,
圆心C(1,1)到直线AB的距离d=r=1即

=1,两边平方得2ab-2ab(b+a)+a
2b
2=a
2+b
2,
∵ab≠0,∴2-2(b+a)+ab=0,∴(a-2)-b-2a+4=2,∴(a-2)(b-2)=2;
由|oA|>2,|OB|>2,可设a-2=m>0,b-2=n>0,且mn=2,
所以S
△AOB=

ab=

(m+2)(n+2)=

(mn+2m+2n+4)≥

(mn+2
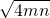
+4)=3+2

,当且仅当m=n即a=b时取等号.
所以三角形AOB面积的最小值为3+2

故答案为:3+2

点评:此题考查学生掌握直线与圆相切时所满足的条件,灵活运用点到直线的距离公式化简求值,会利用基本不等式求函数的最值,是一道中档题.

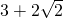
 +
+ =1,即bx+ay-ab=0,
=1,即bx+ay-ab=0, =1,两边平方得2ab-2ab(b+a)+a2b2=a2+b2,
=1,两边平方得2ab-2ab(b+a)+a2b2=a2+b2, ab=
ab= (m+2)(n+2)=
(m+2)(n+2)= (mn+2m+2n+4)≥
(mn+2m+2n+4)≥ (mn+2
(mn+2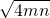 +4)=3+2
+4)=3+2 ,当且仅当m=n即a=b时取等号.
,当且仅当m=n即a=b时取等号.


