
【题目】设圆上的点A(2,3)关于直线x+2y=0的对称点仍在圆上,且直线x-y+1=0被圆截得的弦长为2![]() ,求圆的方程.
,求圆的方程.
【答案】(x-6)2+(y+3)2=52或(x-14)2+(y+7)2=244.
【解析】试题分析:用待定系数法求解。设圆的方程为(x-a)2+(y-b)2=r2,根据圆心在直线![]() 上,点A(2,3)在圆上及弦长得到关于a,b,r的方程组,解方程组求得参数即可得到圆的方程。
上,点A(2,3)在圆上及弦长得到关于a,b,r的方程组,解方程组求得参数即可得到圆的方程。
试题解析:
设圆的方程为(x-a)2+(y-b)2=r2,
由题意,知直线x+2y=0过圆心,
∴a+2b=0.①
又点A在圆上,
∴(2-a)2+(3-b)2=r2.②
∵直线x-y+1=0被圆截得的弦长为![]() ,
,
∴ (![]() )2+
)2+![]() 2=r2.③
2=r2.③
由①②③可得 或
或
故所求圆的方程为(x-6)2+(y+3)2=52或(x-14)2+(y+7)2=244.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了解某校高三毕业生报考体育专业学生的体重(单位:千克)情况,将他们的体重数据整理后得到如下频率分布直方图,已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
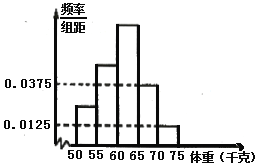
(Ⅰ)求该校报考体育专业学生的总人数![]() ;
;
(Ⅱ)已知A, ![]() 是该校报考体育专业的两名学生,A的体重小于55千克,
是该校报考体育专业的两名学生,A的体重小于55千克, ![]() 的体重不小于70千克,现从该校报考体育专业的学生中按分层抽样分别抽取体重小于55千克和不小于70千克的学生共6名,然后再从这6人中抽取体重小于55千克学生1人,体重不小于70千克的学生2人组成3人训练组,求A不在训练组且
的体重不小于70千克,现从该校报考体育专业的学生中按分层抽样分别抽取体重小于55千克和不小于70千克的学生共6名,然后再从这6人中抽取体重小于55千克学生1人,体重不小于70千克的学生2人组成3人训练组,求A不在训练组且![]() 在训练组的概率.
在训练组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn,且![]() =9,S6=60.
=9,S6=60.
(I)求数列{an}的通项公式;
(II)若数列{bn}满足bn+1﹣bn=![]() (n∈N+)且b1=3,求数列
(n∈N+)且b1=3,求数列![]() 的前n项和Tn.
的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是__________.
①每条直线都有唯一一个倾斜角与之对应,也有唯一一个斜率与之对应;
②倾斜角的范围是:![]() ,且当倾斜角增大时,斜率不一定增大;
,且当倾斜角增大时,斜率不一定增大;
③直线![]() 过点
过点![]() ,且横截距与纵截距相等,则直线
,且横截距与纵截距相等,则直线![]() 的方程一定为
的方程一定为![]() ;
;
④过点![]() ,且斜率为1的直线的方程为
,且斜率为1的直线的方程为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于1 km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,求塔到直路ABC的最短距离.
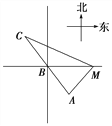
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三梭柱ABC﹣A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1
(1)求证:E是AB中点;
(2)若AC1⊥A1B,求证:AC1⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加书法社团 | 2 | 30 |
(1)从该班随机选 1 名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 8 名同学中,有 5 名男同学![]() ,3名女同学
,3名女同学![]() .现从这 5 名男同学和 3 名女同学中各随机选 1 人,求
.现从这 5 名男同学和 3 名女同学中各随机选 1 人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com