
分析 (1)求出f(x)的最小值,得到关于a的方程,求出a的值即可;
(2)根据不等式的性质,问题转化为m2-2m<3,解出即可.
解答 解:(1)f(x)=|x-1|+|x-a|≥|a-1|,
故|a-1|=3,解得:a=-2或4,
由a>0,得a=4;
(2)由(1)得f(x)=|x-1|+|x-4|,
x≥4时,f(x)=x-1+x-4=2x-5≥3,
1<x<4时,f(x)=x-1-x+4=3,
x≤1时,f(x)=1-x-x+4=-2x+5≥3,
∴f(x)+|x|≥3,当x=0时”=“成立,
故m2-2m<3即(m+1)(m-3)<0,解得:-1<m<3,
故m的范围是(-1,3).
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,转化思想,是一道中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{16}$ | B. | $\frac{1}{16}$ | C. | $\frac{\sqrt{2}}{32}$ | D. | $\frac{1}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
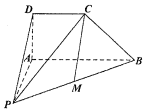 如图,在四棱锥P-ABCD中,CD∥AB,AD=DC=$\frac{1}{2}$AB.
如图,在四棱锥P-ABCD中,CD∥AB,AD=DC=$\frac{1}{2}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{π}$ | B. | $\frac{π}{4}$ | C. | 2-$\frac{2}{π}$ | D. | 2-$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
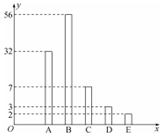 某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为A、B、C、D、E五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:
某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为A、B、C、D、E五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com