
����Ŀ������Ԥ�⣬ij�ص�n��n��N*�����¹���������Ͷ��������ʧ���ֱ�Ϊan��bn����λ������������an= ![]() ��bn=n+5����n���µĹ��������ı�������ǰn���µ��ۼ�Ͷ�������ۼ���ʧ���IJ
��bn=n+5����n���µĹ��������ı�������ǰn���µ��ۼ�Ͷ�������ۼ���ʧ���IJ
��1����õ�����4���µĹ��������ı�������
��2����֪�õع�������ͣ�ŵ��n���µĵ���������Sn=��4��n��46��2+8800����λ������������ij�µף����������������ﵽ����ʸñ������Ƿ��˴�ʱͣ�ŵ�ĵ�����������
���𰸡�
��1���⣺��an=  ��bn=n+5
��bn=n+5
��a1=5��14+15=20
a2=5��24+15=95
a3=5��34+15=420
a4=��10��4+470=430
b1=1+5=6
b2=2+5=7
b3=3+5=8
b4=4+5=9
��ǰ4���¹�Ͷ�ŵ���Ϊa1+a2+a3+a4=20+95+420+430=965��
ǰ4���¹���ʧ����Ϊb1+b2+b3+b4=6+7+8+9=30��
��õ�����4���µĹ��������ı�����Ϊ965��30=935
��2���⣺��an��bn����Ȼn��3ʱ�������
��n��4ʱ���Щ�10n+470��n+5�����n�� ![]() ��
��
���42���µף��������ﵽ���
��n��4��{an}Ϊ����Ϊ��10�Ȳ����У���{bn}Ϊ�Ȳ�Ϊ1�ĵȱ����У�
�ൽ��42���µף�����������Ϊ ![]() ��39+535��
��39+535�� ![]() ��42=
��42= ![]() ��39+535��
��39+535�� ![]() ��42=8782��
��42=8782��
S42=��4��16+8800=8736��
��8782��8736��
���42���µ���������������������
����������1�������{an}��{bn}��ǰ4��͵IJ�ɵó��𰸣���2����an��bn�ó�n��42���ټ����42���µı����������������ɵó����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P��ABCD������ͼ��ͼ��ʾ��������P��ABCD���ĸ���������������ǣ� �� 
A.3
B.2 ![]()
C.6
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽס��ҡ���������λͬѧ��ѡ��һλ�ɼ����ȶ�������ѡ�֣��μ�ɽ��ʡְҵԺУ���ܴ�������ͬ�������¾������ֲ��ԣ��ɼ����������ʾ�����ݱ��������жϣ������ѡΪ�� �� �ɼ�������
�� | �� | �� | �� | |
ƽ���ɼ� | 96 | 96 | 85 | 85 |
����s | 4 | 2 | 4 | 2 |
A.��
B.��
C.��
D.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��x1 �� y1����B��x2 �� y2������Բ ![]() �ϵ����㣬��֪����
�ϵ����㣬��֪���� ![]() =��
=�� ![]() ��
�� ![]() ����
���� ![]() =��
=�� ![]() ��
�� ![]() ������
������ ![]() =0����Բ��������e=
=0����Բ��������e= ![]() �����᳤Ϊ2��OΪ����ԭ�㣮
�����᳤Ϊ2��OΪ����ԭ�㣮
��������Բ�ķ��̣�
�������ʣ���AOB������Ƿ�Ϊ��ֵ������ǣ������֤����������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ĸ���������y=��x����y=�� ![]() ����y=x3 �� ��y=x
����y=x3 �� ��y=x ![]() ��������ѡ2�������¼�����ѡ2��������ͼ�����ҽ���һ�������㡱�ĸ���Ϊ ��
��������ѡ2�������¼�����ѡ2��������ͼ�����ҽ���һ�������㡱�ĸ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
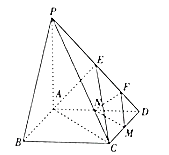
����Ŀ������ͼ��ʾ������ ![]() �У��ı���ABCDΪ�����Σ�
�У��ı���ABCDΪ�����Σ� ![]() ƽ��PAB,��
ƽ��PAB,�� ![]() �ֱ�Ϊ
�ֱ�Ϊ ![]() ���е㣬
���е㣬 ![]() .
.
֤����
��1��![]() ƽ
ƽ ![]() ;
;
��2���� ![]() ��������
�������� ![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
�� ![]() ��
�� ![]() ������
������ ![]() ��
�� ![]() ��ֱ����
��ֱ���� ![]() .
.
��1�������� ![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2�������� ![]() ����
���� ![]() ��������
�������� ![]() ��ǰ
��ǰ ![]() ���
��� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=x3��2ex2+mx��lnx����g��x��= ![]() ��������g��x�����ٴ���һ����㣬��ʵ��m��ȡֵ��Χ�ǣ� ��
��������g��x�����ٴ���һ����㣬��ʵ��m��ȡֵ��Χ�ǣ� ��
A.�����ޣ�e2+ ![]() ]
]
B.��0��e2+ ![]() ]
]
C.��e2+ ![]() ��+��]
��+��]
D.����e2�� ![]() ��e2+
��e2+ ![]() ]
]
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com