
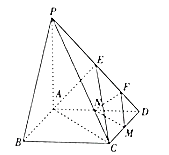
【题目】在如图所示的四棱锥 ![]() 中,四边形ABCD为正方形,
中,四边形ABCD为正方形, ![]() 平面PAB,且
平面PAB,且 ![]() 分别为
分别为 ![]() 的中点,
的中点, ![]() .
.
证明:
(1)![]() 平
平 ![]() ;
;
(2)若 ![]() ,求二面角
,求二面角 ![]() 的余弦值.
的余弦值.
【答案】
(1)解: 证明: 连结BD,分别的交 ![]() 于点
于点 ![]() ,连结
,连结 ![]()
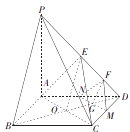
![]() 为BD中点, E为PD中点,
为BD中点, E为PD中点, ![]() .又
.又 ![]() 为ED中点,
为ED中点,
又 ![]() 为OD的中点,
为OD的中点, ![]()
![]() 平面
平面 ![]() 平面
平面 ![]() 平面FMN.
平面FMN.
(2)解: ![]() 平面
平面 ![]() ,又
,又 ![]() 平面
平面 ![]() .
.
如图,以A为坐标原点, ![]() 所在直线分别为x轴、y轴、z轴轴建立空间直角坐标系,
所在直线分别为x轴、y轴、z轴轴建立空间直角坐标系,
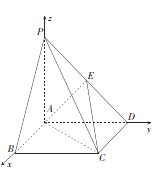
则 ![]() ,则
,则 ![]()
![]() 平面ABCD,
平面ABCD,
![]() 平面ABC的一个法向量
平面ABC的一个法向量 ![]() ,设平面AEC的法向量为
,设平面AEC的法向量为 ![]() ,
,
则 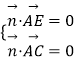 ,即
,即 ![]() ,
,
令x=1,则 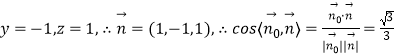 ,
,
由图可知,二面角 ![]() 为饨角,
为饨角, ![]() 二面角
二面角 ![]() 的余弦值
的余弦值 ![]()
【解析】(1)结合题意作出辅助线,由题中的长度关系可得证BP∥FG,由线面平行的判定定理即可证出P B ∥ 平面FMN.(2)根据题意建立空间直角坐标系,求出各个点的坐标进而求出各个向量的坐标,设出平面ABCD和平面EAC的法向量,由向量垂直的坐标运算公式可求出法向量,再利用向量的数量积运算公式![]() 求出余弦值即可。
求出余弦值即可。
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C1: ![]() =1和C2:x2+
=1和C2:x2+ ![]() =1.P为C1上的动点,Q为C2上的动点,w是
=1.P为C1上的动点,Q为C2上的动点,w是 ![]() 的最大值.记Ω={(P,Q)|P在C1上,Q在C2上,且
的最大值.记Ω={(P,Q)|P在C1上,Q在C2上,且 ![]() =w},则Ω中元素个数为( )
=w},则Ω中元素个数为( )
A.2个
B.4个
C.8个
D.无穷个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据预测,某地第n(n∈N*)个月共享单车的投放量和损失量分别为an和bn(单位:辆),其中an= ![]() ,bn=n+5,第n个月底的共享单车的保有量是前n个月的累计投放量与累计损失量的差.
,bn=n+5,第n个月底的共享单车的保有量是前n个月的累计投放量与累计损失量的差.
(1)求该地区第4个月底的共享单车的保有量;
(2)已知该地共享单车停放点第n个月底的单车容纳量Sn=﹣4(n﹣46)2+8800(单位:辆).设在某月底,共享单车保有量达到最大,问该保有量是否超出了此时停放点的单车容纳量?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若样本![]() 的平均数是
的平均数是![]() ,方差是
,方差是![]() ,则对样本
,则对样本![]() ,下列结论正确的是 ( )
,下列结论正确的是 ( )
A. 平均数为14,方差为5 B. 平均数为13,方差为25
C. 平均数为13,方差为5 D. 平均数为14,方差为2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A为椭圆 ![]() =1(a>b>0)上的一个动点,弦AB,AC分别过左右焦点F1 , F2 , 且当线段AF1的中点在y轴上时,cos∠F1AF2=
=1(a>b>0)上的一个动点,弦AB,AC分别过左右焦点F1 , F2 , 且当线段AF1的中点在y轴上时,cos∠F1AF2= ![]() . (Ⅰ)求该椭圆的离心率;
. (Ⅰ)求该椭圆的离心率;
(Ⅱ)设 ![]() ,试判断λ1+λ2是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
,试判断λ1+λ2是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com