
【题目】已知A为椭圆 ![]() =1(a>b>0)上的一个动点,弦AB,AC分别过左右焦点F1 , F2 , 且当线段AF1的中点在y轴上时,cos∠F1AF2=
=1(a>b>0)上的一个动点,弦AB,AC分别过左右焦点F1 , F2 , 且当线段AF1的中点在y轴上时,cos∠F1AF2= ![]() . (Ⅰ)求该椭圆的离心率;
. (Ⅰ)求该椭圆的离心率;
(Ⅱ)设 ![]() ,试判断λ1+λ2是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
,试判断λ1+λ2是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
【答案】解:(Ⅰ)当线段AF1的中点在y轴上时,AC垂直于x轴,△AF1F2为直角三角形.
因为cos∠F1AF2= ![]() ,所以|AF1|=3|AF2|,易知|AF2|=
,所以|AF1|=3|AF2|,易知|AF2|= ![]() ,
,
由椭圆的定义可得|AF1|+|AF2|=2a,
则4 ![]() =2a,即a2=2b2=2(a2﹣c2),即a2=2c2,
=2a,即a2=2b2=2(a2﹣c2),即a2=2c2,
即有e= ![]() =
= ![]() ;
;
(Ⅱ)由(Ⅰ)得椭圆方程为x2+2y2=2b2,焦点坐标为F1(﹣b,0),F2(b,0),
⑴当AB,AC的斜率都存在时,设A(x0,y0),B(x1,y1),C(x2,y2),
则直线AC的方程为y= ![]() (x﹣b),代入椭圆方程得
(x﹣b),代入椭圆方程得
(3b2﹣2bx0)y2+2by0(x0﹣b)y﹣b2y02=0,
可得y0y2=﹣ ![]() ,又λ2=
,又λ2= ![]() =
= ![]() =
= ![]() ,
,
同理λ1= ![]() ,可得λ1+λ2=6;
,可得λ1+λ2=6;
⑵若AC⊥x轴,则λ2=1,λ1= ![]() =5,这时λ1+λ2=6;
=5,这时λ1+λ2=6;
若AB⊥x轴,则λ1=1,λ2=5,这时也有λ1+λ2=6;
综上所述,λ1+λ2是定值6.
【解析】(Ⅰ)当线段AF1的中点在y轴上时,AC垂直于x轴,△AF1F2为直角三角形.运用余弦函数的定义可得|AF1|=3|AF2|,易知|AF2|= ![]() ,再由椭圆的定义,结合离心率公式即可得到所求值;
,再由椭圆的定义,结合离心率公式即可得到所求值;
(Ⅱ)由(Ⅰ)得椭圆方程为x2+2y2=2b2,焦点坐标为F1(﹣b,0),F2(b,0),(1)当AB,AC的斜率都存在时,设A(x0,y0),B(x1,y1),C(x2,y2),求得直线AC的方程,代入椭圆方程,运用韦达定理,再由向量共线定理,可得λ1+λ2为定值6;若AC⊥x轴,若AB⊥x轴,计算即可得到所求定值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,△ABC的面积为S,(a2+b2)tanC=8S,且sinAcosB=2cosAsinB,则cosA= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|2x﹣3|<x与不等式x2﹣mx+n<0的解集相同. (Ⅰ)求m﹣n;
(Ⅱ)若a、b、c∈(0,1),且ab+bc+ac=m﹣n,求a+b+c的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣ax,在x=
x3﹣ax,在x= ![]() 处取得极小值,记g(x)=
处取得极小值,记g(x)= ![]() ,程序框图如图所示,若输出的结果S>
,程序框图如图所示,若输出的结果S> ![]() ,则判断框中可以填入的关于n的判断条件是( )
,则判断框中可以填入的关于n的判断条件是( ) 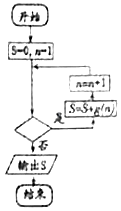
A.n≤12?
B.n>12?
C.n≤13?
D.n>13?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节来临,有农民工兄弟A、B、C、D四人各自通过互联网订购回家过年的火车票,若订票成功即可获得火车票,即他们获得火车票与否互不影响.若A、B、C、D获得火车票的概率分别是 ![]() ,其中p1>p3 , 又
,其中p1>p3 , 又 ![]() 成等比数列,且A、C两人恰好有一人获得火车票的概率是
成等比数列,且A、C两人恰好有一人获得火车票的概率是 ![]() .
.
(1)求p1 , p3的值;
(2)若C、D是一家人且两人都获得火车票才一起回家,否则两人都不回家.设X表示A、B、C、D能够回家过年的人数,求X的分布列和期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班抽取20名学生周测物理考试成绩(单位:分)的频率分布直方图如下:
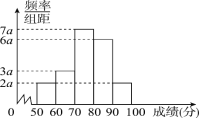
(1)求频率分布直方图中a的值,并写出众数;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生中任选2人,求这2人的成绩都在[60,70)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,其中a∈R. (Ⅰ)给出a的一个取值,使得曲线y=f(x)存在斜率为0的切线,并说明理由;
,其中a∈R. (Ⅰ)给出a的一个取值,使得曲线y=f(x)存在斜率为0的切线,并说明理由;
(Ⅱ)若f(x)存在极小值和极大值,证明:f(x)的极小值大于极大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com