
已知复数z=cos2α+isinα,α∈R,且argz=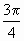 ,
,
(Ⅰ)求复数z;
(Ⅱ)若复数ω满足|ω|=1,且|z-ω|≤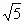 ,求argω的范围.
,求argω的范围.
|
本小题主要考查复数的概念和三角基本运算. 解:(Ⅰ)由argz= ∴2sin2α-sinα-1=0, 解得sinα=- ∵sinα>0,∴舍去sinα=- 故z=-1+i. (Ⅱ)由|ω|=1可设ω=cosθ+isinθ, 得z-ω=(-1-cosθ)+(1-sinθ)i, ∴|z-ω|= ∵|z-ω|≤ ∴3+2 又θ=argω∈[0,2π), ∴ 于是0≤θ≤ |


科目:高中数学 来源:2004全国各省市高考模拟试题汇编(天利38套)·数学 题型:044
已知复数z=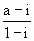 其中a>0,i为虚数单位.复数u=z(z+i)的虚部减去它的实部所得的差等于
其中a>0,i为虚数单位.复数u=z(z+i)的虚部减去它的实部所得的差等于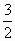 ,求复数u的模.
,求复数u的模.
查看答案和解析>>
科目:高中数学 来源:2010-2011年河南省许昌市四校高二下学期第一次联考文科数学 题型:解答题
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17. (本小题满分10分)
已知复数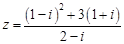 ,若
,若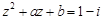 ,
,
⑴求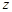 ;
;
⑵求实数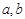 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com