
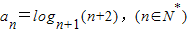 ,定义使a1a2a3…ak为整数的数k(k∈N*)叫做数列{an}的企盼数,则区间[1,2009]内的所有企盼数的和为 .
,定义使a1a2a3…ak为整数的数k(k∈N*)叫做数列{an}的企盼数,则区间[1,2009]内的所有企盼数的和为 . 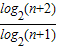
 ×
× …×
…×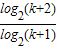 =log2(k+2),
=log2(k+2),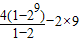 =2026
=2026

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省中山市纪念中学高三(上)9月月考数学试卷(理科)(解析版) 题型:填空题
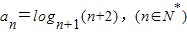 ,定义使a1a2a3…ak为整数的数k(k∈N*)叫做数列{an}的企盼数,则区间[1,2009]内的所有企盼数的和为 .
,定义使a1a2a3…ak为整数的数k(k∈N*)叫做数列{an}的企盼数,则区间[1,2009]内的所有企盼数的和为 .查看答案和解析>>
科目:高中数学 来源:江西省月考题 题型:单选题
查看答案和解析>>
科目:高中数学 来源:期末题 题型:填空题
 a2
a2 a3
a3 …
… ak为整数的数k(k∈N+)叫做幸运数,则k∈[1,2011]内所有的幸运数的和为( ).
ak为整数的数k(k∈N+)叫做幸运数,则k∈[1,2011]内所有的幸运数的和为( ). 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com